Detection and Estimation (Lec 1~6 summary)

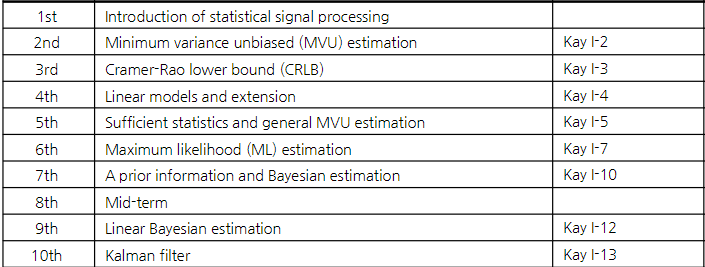
GIST 황의석 교수님 [EC7204-01] Detection and Estimation 강의 정리 내용입니다.

Estimation: 연속적 가설, 예측 오차 최소화
Detection: 이산적 가설, 명확한 맞음/틀림

Lec 2: Minimum Variance Unbiased Estimation (MVUE)

Unbiased Estimator: 기대치가 참값과 동일한 추정기
- Unbiased estimator is not necessarily a good estimator;
  
  but a biased estimator is a poor estimator.
Mean Squared Error (MSE): 분산과 바이어스 제곱의 합으로 구성
- MSE Criterion
  
  $\text{mse}(\hat{\theta}) = E\left[(\hat{\theta} - \theta)^2\right]$
  
  $\quad\quad\quad = E\left[\left((\hat{\theta} - E(\hat{\theta})) + (E(\hat{\theta}) - \theta)\right)^2\right]$
  
  $\quad\quad\quad = \text{var}(\hat{\theta}) + \left[E(\hat{\theta}) - \theta\right]^2$
  
  $\quad\quad\quad = \text{var}(\hat{\theta}) + b^2(\theta)$
MVUE: 비편향 조건 하에 분산을 최소화한 추정기
- MVUE의 조건: $\text{Bias}(\hat{\theta}) = 0$ 이고, $\text{Var}(\hat{\theta})$ 최소화

Lec 3. Cramer-Rao Lower Bound (CRLB)

Cramer-Rao Lower Bound (CRLB)

CRLB는 비편향 추정기의 분산에 대한 하한을 제공
Fisher Information($I(\theta)$)로 CRLB 정의:

\[\text{Var}(\hat{\theta}) \ge \frac{1}{{I(\theta)}},\quad I(\theta) = - E[\frac{\partial^2}{\partial \theta^2}\text{ln}f(x;\theta)] = E[(\frac{\partial}{\partial \theta}\text{ln} f(x;\theta))^2]\]
The CRLB give a lower bound on the variance of any unbiased estimator. (biased의 경우는 알 수 없다!)
Does not guarantee bound can be obtained.
만약 unbiased estimator의 variance가 CRLB라면 그 estimator는 MVUE.

Theorem: CRLB - Scalar Parameter

Let $p(\mathbf{x}; \theta)$ satisfy the “regularity” condition

\[E_\mathbf{x}[\frac{\partial\text{ln}\ p(\mathbf{x}; \theta)}{\partial \theta}] = 0\quad \text{for all}\ \theta\]

Then, the variance of any unbiased estimator $\hat{\theta}$ must satisfy

\[\text{var}(\hat{\theta}) \ge \frac{1}{-E_\mathbf{x}[\frac{\partial^2\text{ln}\ p(\mathbf{x}; \theta)}{\partial \theta^2}]} = \frac{1}{E_\mathbf{x}[(\frac{\partial\text{ln}\ p(\mathbf{x}; \theta)}{\partial \theta})^2]} = \frac{1}{I(\theta)}\]

where the derivative is evaluated at the true value $\theta$ and the expectation is taken w.r.t. $p(\mathbf{x};\theta).$

여기서 세번째 텀에서 - 가 사라지는 이유는, 두번째 텀에서 - 가 붙는 이유를 생각해보면 된다.

두번째 텀에서 마이너스가 붙는 이유는 값을 양수로 만들어주기 위함이고, 세번째 텀은 일차 미분의 제곱이므로 자연스럽게 양수이다. 따라서 - 가 사라지게 된다.

Furthermore, an unbiased estimator may be found that attains the bound for all $\theta$ if and only if

\[\frac{\partial\ \text{ln}\ p(\mathbf{x}; \theta)}{\partial \theta} = I(\theta)(g(\mathbf{x})-\theta)\]

for some functions $g()$ and $I$. That estimator, which is the MVUE, is $\hat{\theta} = g(\mathbf{x})$, and the minimum variance is $\frac{1}{I(\theta)}$

이렇게 표현이 되면 g() 는 MVUE 이다.
Fisher Information: 추정 정확도를 측정하는 방법. 우도 함수의 곡률이 크면 추정량의 분산이 작고, 더 정확한 추정을 할 수 있음을 의미
정칙성 조건(Regularity Conditions): CRLB가 성립하기 위한 조건으로, 특정 미분 가능성 조건을 만족해야 한다.

CRLB True or False

The CRLB always exists regardless of $p(\mathbf{x}; \theta).$

(F) - regularity condition을 만족해야함 → Fisher information을 계산해야 하는데 $p(x;\theta)$가 충분히 매끄럽고 미분 가능해야 하기 때문
The CRLB applies to unbiased estimators only.

(T)
Determining the CRLB requires statistics of all possible estimators $\hat{\theta}$.

(F) CRLB를 계산하기 위해서는 가능도 함수(Likelihood function)와 Fisher Information만 필요. 모든 가능한 추정량의 통계를 알 필요는 없다.
The CRLB depends on the observations $\mathbf{x}$

(F) CRLB는 파라미터 $\theta$와 관측된 데이터 분포를 기반으로 Fisher Information을 계산하는 것이지, 개별 관측값 $x$에 의존하지 않는다. 이는 분포 수준에서 정의된다.
The CRLB depends on the parameter to be estimated, $\theta$.

(T) CRLB는 추정하려는 파라미터 $\theta$와 Fisher Information에 따라 달라진다. Fisher Information 자체가 $ $에 의존하기 때문
The CRLB tells you whether or not a MVUE exists.

(F) CRLB는 MVUE의 존재 여부를 알려주지 않는다. MVUE의 존재 여부는 Rao-Blackwell 정리 및 Lehmann-Scheffe 정리와 같은 다른 이론에 의해 결정

Lec 4. Linear Models and Extensions

Linear estimator와 다름 Linear estimation이 based $x$ 라면 Linear model은 based A, B ($\theta$)
Line fitting example

$x[n] = A+Bn + w[n], \quad n=0,1,...,N-1,\quad w[n]:\text{WGN}$

In Matrix notation,

$\mathbf{x=H\theta+w}$ : linear model

$\mathbf{x} = [x[0]\ x[1]\ ...\ x[N-1]]^T$

$\mathbf{w} = [w[0]\ w[1]\ ...\ w[N-1]]^T\quad \mathbf{w\sim \cal{N}(\mathbf{0}, \sigma^2\mathbf{I})}$

$\mathbf{\theta} = [A\ B]^T$

$\mathbf{H} = \begin{bmatrix} 1 & 0 \\ 1 & 1 \\ \vdots & \vdots \\ 1 & N-1 \end{bmatrix}$
선형 모델 ($y = A\theta + n$) 에서 MVUE 찾기
CRLB 이론을 통해 선형 모델의 MVUE 계산:

\[\hat{\theta} = (H^TH)^{-1}H^T\mathbf{x}, \quad \text{Cov}(\hat{\theta}) = \sigma^2(H^TH)^{-1}\]

Lec 5. General MVU Estimator

Sufficiency(충분 통계량)

주어진 데이터에서 추정하고자 하는 모수(parameter)에 관한 모든 정보를 포함하고 있는 통계량

원래 데이터 전체를 사용하는 것과 동일한 추론 결과를 제공하며, 데이터의 크기를 줄이는 동시에 정보의 손실을 최소화하는 역할
통계량 $T(X)$가 주어진 데이터 $X$에 대해 모수 $\theta$의 충분 통계량이 되기 위한 조건은 Neyman-Fisher Factorization Theorem를 따른다.

\[f(x;\theta) = g(T(x),\theta)h(x), \quad T(x):\text{충분 통계량}\]

즉, 원래 데이터의 확률 분포 $f(x;\theta)$가 $T(X)$로 축약되었을 때 동일한 정보를 제공한다면 $T(X)$는 충분 통계량
Completeness(완전성, 완비성)

충분 통계량과 관련된 개념으로, 주어진 통계량이 모수(parameter)에 대한 정보를 얼마나 완전하게 담고 있는지를 나타낸다.

통계량 $T(X)$가 완비 통계량이라는 것은, 만약 $T(X)$의 함수 $g(T(X))$가 다음 조건을 만족한다면 $g(T(X))=0$이 항상 성립해야 한다는 것을 의미한다

\[E[g(T(X))] = 0 \quad \text{for all } \theta \implies g(T(X)) = 0 \quad \text{almost surely}.\]
- 완비성의 직관 - 완비성은 통계량 $T(X)$가 모수와 관련된 불필요한 정보를 포함하지 않는다는 것을 보장. 즉, 통계량이 모수에 대한 “모든” 정보를 포함하고 있고, 이 정보를 사용해 더 이상 모수와 독립적인 추가 정보를 도출할 수 없음을 의미
모든 충분 통계량이 Completeness한 것은 아니다.
Rao-Blackwell-Lehmann-Scheffe 정리를 사용한 MVUE 계산
1. $T(X)$가 $\theta$에 대한 완비 충분 통계량이고
2. $\hat{\theta}(X)$가 $\theta$에 대한 편향되지 않은 추정량이라면,
조건부 기댓값

\[\hat{\theta}_{\text{MVU}} = E[\check{\theta} | T(\mathbf{x})],\quad T(\mathbf{x}):\text{충분 통계량}\]

는 $\theta$에 대한 MVUE 이다.

Lec 6. Maximum Likelihood Estimation (MLE)

MLE는 관측된 데이터를 가장 잘 설명하는 매개변수를 선택

\[\hat{\theta}_{\text{MLE}} = \text{argmax}_{\theta}\text{ln}\ p(x;\theta)\]

대표본에서는 MLE가 비편향, 효율적.