Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains(2020)

기존의 Coordinate-based MLPs가 low frequencies는 잘 학습하지만 high frequencies는 잘 학습하지 못하는 “spectral bias” 라는 현상을 Fourier features mapping을 통해 극복하고 이를 Neural Tangent Kernel 이론으로 설명한 논문
적용이 간단한데 강력하고, 이론도 탄탄한 논문

왼쪽은 그냥 coordinate-based MLPs, 오른쪽은 Fourier features mapping을 사용한 MLPs의 결과
어떻게 Test PSNR이 존재하는가? → 일부 픽셀은 train으로, 일부 픽셀은 test로 사용

Coordinate-based MLP

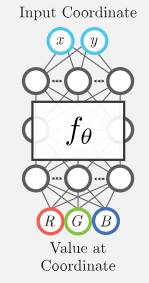
특정한 입력 (예: 좌표값)을 기반으로 출력을 예측하는 MLP
주로 신호를 모델링하거나, 이미지 복원, 3D 신호 복원 등 다양한 응용 분야에서 사용된다.
입력: 저차원 좌표값(\(R^3\) 내의 포인트)
출력: 주어진 좌표에 대한 함수값(이미지의 픽셀 값, 신호의 세기 등)
활용 분야: NeRF(Neural Radiance Fields)나 Implicit Neural Representations와 같은 분야에서 널리 사용

Coordinate-based MLP의 문제점

고주파를 학습하는 데 어려움을 겪음. 이를 “spectral bias”라고 한다.
1. 학습이 잘 안되던 이유를 NTK를 통해 알아볼 것임.
2. spectral bias를 input(x, y 좌표)값에 Fourier feature mapping을 하여서 해결할 것임.

NTK 이해를 위해 간단히 짚고 넘어가자.

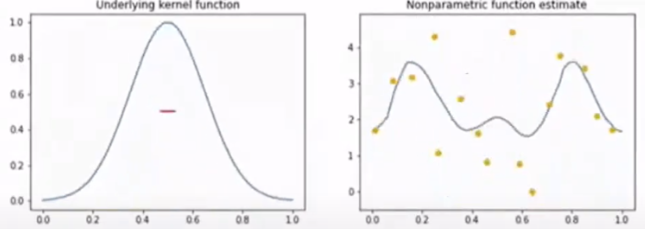
Kernel regression

input, output data를 받아서 이를 만족하는 continuous function을 추정하는 것을 목표로 하는 task.
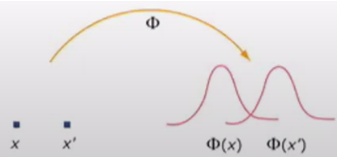
어떤것을 커널 function으로 고르냐도 중요하고 표준편차도 중요하다. (kernel의 width는 표준편차 \(\sigma\) 에 의해 결정된다.)

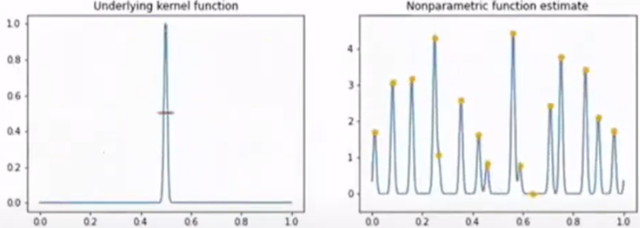
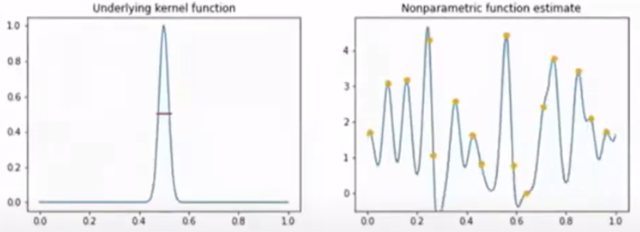
Kernel Trick

고차원 매핑 + 내적 = kernel!
Linearly inseparable 한 data point \(x\) 에 대하여 \(\phi (x)\)(:feature map) 는 linear separability를 갖게 만드는 non-linear mapping function 이라고 하자.

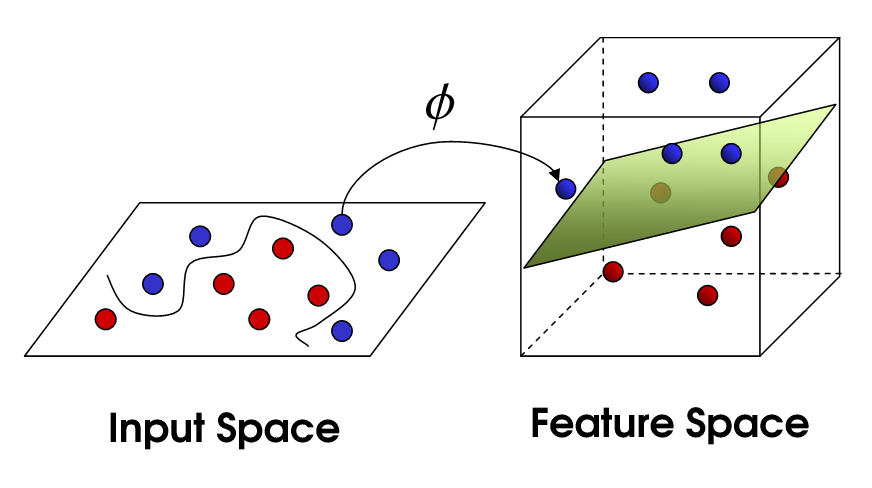
이때 kernel trick은 이러한 feature map을 explicit 하게 구하지 않고, kernel을 통해서 feature space를 구하는 kernel regression이며, 다음과 같이 정의한다.

\[K(x,x')=\phi(x)^T\phi(x')\]

이는 input \(x\) 에 feature mapping을 거친 후에 내적을 취해준다기 보단, kernel을 통해 좋은 성질을 갖는 feature map \(\phi\) 를 구할 수 있다고 해석하는 편이 좋다.

Neural Tangent Kernel(NTK)

Neural Network의 학습을 하면서 거치는 과정에 대한 특징을 매우 정확하게 묘사할 수 있다는 방법

한 레이어에 넓은 width를 가진 뉴런의 학습에서 추정되는 function이 알고있는 커널(여기선 NTK)을 사용한 kernel regression을 수행하는 것과 동치라는 점을 이론적으로 밝힘.

\[f(w,x)\approx f(w_0,x)+\nabla_w f(w_0,x)^T(w-w_0)+...\]

어떠한 neural network model을 위와 같은 linearization으로 표현할 수 있다. 이때 Taylor expanded tangent line은 다음과 같은 성질을 가진다.
1. weight \(w\) 에 대해서 linear
2. \(x\) 에 대해서 non-linear
이에 따라 tangent line의 gradient term \(\nabla_w f(w_0,x)^T(w-w_0)\) 을 다음과 같이 해석 가능.

\(\phi(x)=\nabla_w f(w_0,x)\) : non-linear data point \(x\) 를 어떠한 유용한 space에 mapping 하는 feature map.

이에 해당하는 kernel \(K\) 는 다음과 같이 정의할 수 있다.

\[K(x_i, x_j) = h_{\text{NTK}} = <\phi(x_i), \phi(x_j)> = \nabla_wf(w_0,x)^T\nabla_wf(w_0,x)\]

이때, 정의된 neural tangent kernel을 neural network의 gradient descent에서 찾을 수 있다.

timestep \(t\) 에 대하여 gradient descent를 다음과 같이 표현해보자.

\[w(t+1) = w(t) - \eta \nabla_w l\]

\[\rightarrow \frac{w(t+1)-w(t)}{\eta}=-\nabla_w l \approx \frac{dw}{dt}\]

이제 loss function이 MSE 일 때, 다음과 같이 \(\nabla_w l\) 를 구할 수 있고

\[l(w)=\frac{1}{2}||f(w,x)-y||^2\]

\[\rightarrow \nabla_w l = \nabla_w f(w,x)\cdot (f(w,x)-y)= -\frac{dw}{dt}\]

이에 따라 optimization-based neural network training을 다음과 같이 NTK로 나타낼 수 있다.

\[y(w)=f(w,x)\approx f(w_0,x)+\nabla_w f(w_0,x)^T(w-w_0)\]

\[\frac{d}{dt}y(w)=\nabla_w f(w,x)^T\cdot \frac{d}{dt}w \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \]

\[= -\nabla_w f(w, x)^T\cdot \nabla_w f(w,x)(f(w,x)-y)\]

\[= -h_{\text{NTK}}(f(w,x)-y)\quad \quad \quad \quad \quad \quad \quad \quad \]

이제 \(u=y(w)-y\) 라고 하자. 이 때, training iteration \(t\) 에서의 output residual을 다음과 같이 표현할 수 있다. (1차 선형 미분 방정식)

\[u(t)=u(0)\text{exp}(-\eta h_{\text{NTK}}t)\]

이제 논문에서의 Eq.3을 살펴보자.

위에서 살펴보았던 NTK approximation에 따라, test data \(\bf{X}_{\text{test}}\) 에 대해 \(t\) iteration 이후의 network의 prediction은 다음과 같이 표현할 수 있다.

\[\hat{{\bf{y}}}^{(t)} \approx {\bf{K}}_{\text{test}}{\bf{K}}^{-1}({\bf{I}}-e ^{-\eta{\bf{K}}t}){\bf{y}}\]

이상적인 training에 대해서 \(\bf{K}_{\text{test}}=\bf{K}\) 가 성립할 것이기 때문에 \(u(t)=u(0)\text{exp}(-\eta h_{\text{NTK}}t)\) 의 residual을 통해 output을 포현한 것과 같은 형태임을 알 수 있다.

이제 우리는 NTK kernel을 eigendecomposition 하여 \(\bf{K=Q\Lambda Q^T}\) 로 나타낼 때, 위 식을 다음과 같이 표현할 수 있다.

\[\bf{Q^T(}\hat{{\bf{y}}}^{(t)}-y) \approx {\bf{Q^T(K}}_{\text{test}}{\bf{K}}^{-1}({\bf{I}}-e ^{-\eta{\bf{K}}t}){\bf{y-y}})\]

\[\approx {\bf{Q^T}}(({\bf{I}}-e^{-\eta {\bf{K}}t})\bf{y-y))}\]

\[\approx -e^{-\eta \Lambda t}{\bf{Q}^Ty} \quad (\because e^{-\eta \Lambda t} = {\bf{Q}}e^{-\eta \Lambda t} \bf{Q}^T)\]

따라서 우리는 exponential의 지수 항이 eigenvalue 값에 따라 decay 됨을 알 수 있고, 이는 즉 larger eigenvalue가 더 빨리 학습함을 의미한다.

그러면 여기서 MLP가 고주파를 잘 학습하지 못하는 이유가 나온다.

많은 ‘자연적’ 형태와 신호는 \(\frac{1}{f^p}\) 주파수 스펙트럼을 갖는다. (Frequency synthesis is based upon the observation that many “natural” forms and signals have a 1/fp frequency spectra) - 빈도가 높으면 고유값이 큰가? 확인 必

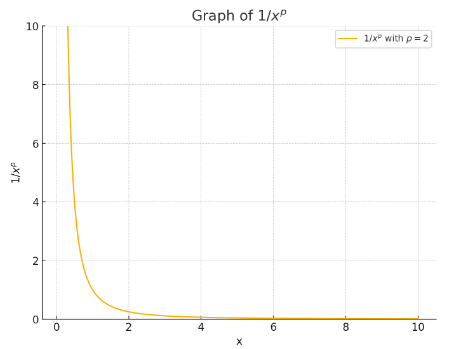
2019년의 한 논문 “The convergence rate of neural networks for learned functions of different frequencies.”에 따르면,

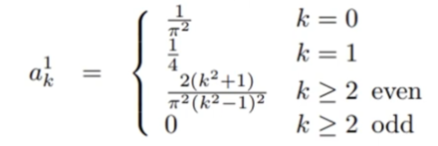
주파수 k에 따라 고유값은 다음과 같은 값을 갖는다고 한다.

즉, low frequency 일수록 eigen value \(\lambda_L\) 는 큰 값을 가지고, high frequency 일수록 eigen value \(\lambda_H\) 는 작은 값을 가진다고 한다. High frequency의 eigen value가 작기 때문에 학습이 잘 되지 않던 것!

여기까지 MLP가 고주파를 잘 학습하지 못하는 이유에 대해 알아보았다.
NN을 하나 정했다고 하면, 이 NN에 따라서 정해지는 NTK는 오직 하나이다. 즉, analytic한 kernel.

위에서 보았듯 학습이 잘 되기 위해선 적절한 kernel의 width가 설정되어야 한다.

하지만 NN의 무엇을 조절해야 kernel width를 조절할 수 있는지 불명확. 여기서 쓸 수 있는게 Fourier features mapping 이다.

Fourier Features Mapping

Random features for large-scale kernel machines, NIPS 2007 에서 나온 내용

Fourier featuring: coordinate space point를 frequency space로 embedding 하는 function의 총칭
Fourier feature mapping 이라는 것을 통해서 input coordinate를 바꿔주면 kernel width를 목적에 맞도록 변화시키는 것이 가능!

즉 kernel의 width가 바뀌는 것을 tuning 할 수 있다.
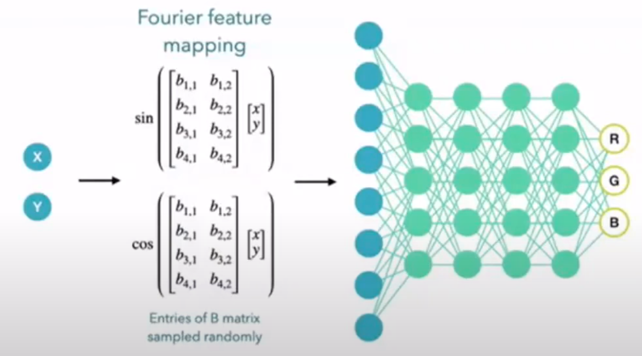
Mapping: \(\gamma(\bf{x})=(\text{sin}(\bf{B}x), \text{cos}(\bf{B}x))\)

여기서 \(\bf{B}\) 는 주기를 조절할 수 있는 Scaling 값이다.
Fourier features mapping이 width를 조절하는 걸 tuning 할 수 있는 손쉬운 방법이며 이걸 잘 조절할 수 있어야 얼마나 데이터에 fitting을 잘 할 수 있는지도 조절이 가능하다. 목적에 맞도록 width를 바꿀 수 있다는게 이 논문의 contribution.

인풋에 fourier feature mapping을 한 예시)

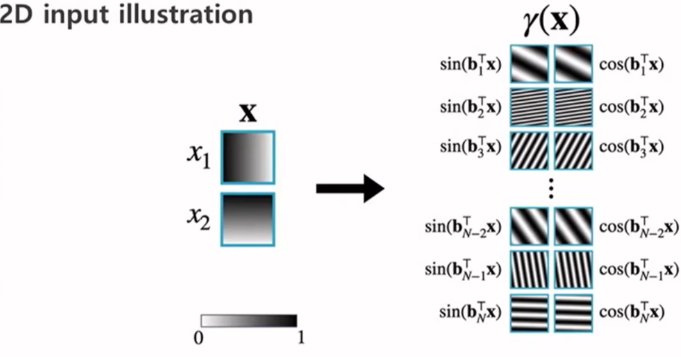
meshgrid. 왼쪽에서 오른쪽으로 갈수록 값이 커짐

<직관>

원래는 \(x_1\) 에서 하나 뽑고 \(x_2\) 에서 하나 뽑고 대응되는 RGB 값을 output으로 내는데

이를 주파수가 다양한 fourier basis function들을 만들어서 이것들의 weighted sum을 통해 output을 만들어내도록 해주는 것이기 때문에 그냥 (x, y) 좌표를 주는 것보다 잘한다.

<이론>

이렇게 하는 것이 왜 좋은가? NTK로 분석

MLP에 대응하는 NTK가 있을 것. (analytic하게 하나가 딱 생김)
NTK는 input vector간의 내적에 대한 스칼라 function \(h\)로 composite하게 표현이 가능(증명을 통해 나온 결과)

\[\text{NTK}(x,y)=h(x^{T}y)\]

\(x\)와 \(y\)에 각각 Fourier feature mapping \(\gamma\) 를 씌우고 Dot 내적 하면

\[\gamma(x)^T \gamma(y)=\text{sin}(\bf{B}x)^T\text{sin}(\bf{B}y)+\text{cos}(\bf{B}x)^T\text{cos}(\bf{B}y)=\text{cos}(\bf{B}(x-y))\]

\[\text{NTK}(\gamma(x), \gamma(y))=h(\text{cos}(\bf{B}(x-y)))\]

이 매핑한 값 \(\gamma(x)\), \(\gamma(y)\)를 내적한 것이 어떤 의미를 가지는가?

→ kernel이 stationary하다. 원래 \(\text{NTK}(x,y)\) 는 stationary하지 않은데 Fourier feature mapping을 하는 순간 NTK 커널이 stationary 하게 됐다는게 좋은 점

차이 값에만 dependent하며 \(x\) 나 \(y\) 값이 어떤 값인지는 상관이 없다. (shift invariant, time invariant…)

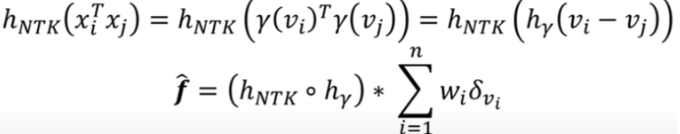
또한 다음과 같이 MLP 연산이 convolution이 되므로 기존 MLP와는 달리 global하게 학습할 수 있게 된다고 한다.

여기서 등장한 B가 kernel의 width를 조절할 수 있게 되었다. (나머지는 다 fix, B만 바꾸기만 해도 커널의 width를 조절할 수 있게 됨)

Kernel이 넓은 것은 Fourier feature scale \(\sigma\) 가 작은 것과 대응이 된다. (underfitting)

Kernel이 좁은 것은 Fourier feature scale \(\sigma\) 가 큰 것과 대응이 된다. (overfitting, 잡음이 너무 fitting 됨)
- 이해를 위한 설명.
  
  Time series data에서 주파수를 확인하고 싶으면 일정구간을 잡고 Fourier transform을 하면 됨.
  
  다만 너무 길게 잡으면 time resolution이 너무 커서 어느 부분(어느 시간)에 이 주파수가 나왔는 지 파악이 어려움.
  
  그렇다고 짧게 짧게 윈도잉해서 Fourier transform을 하면, Window보다 긴 신호는 얻어낼 수 없다. tradeoff 관계(time resolution은 좋아졌으나 fourier domain에서의 resolution은 안좋아짐)
그러면 이 \(\bf{B}\)를 어디서 뽑는가? 지금은 가우시안에서 뽑고있는데 라플라시안이나 유니폼 등에서도 뽑을 수 있는가?

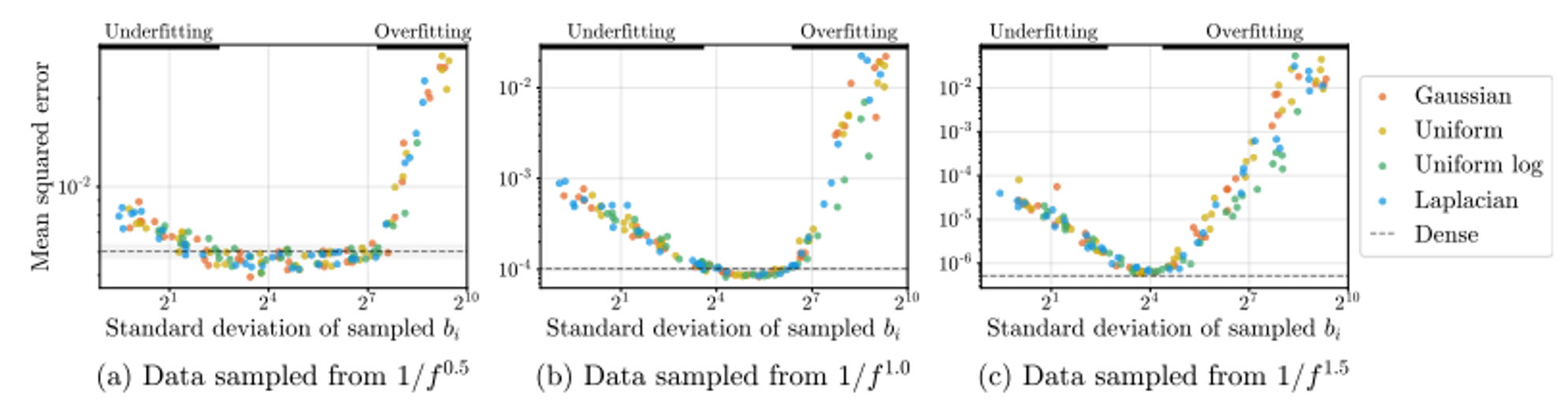
어떤 분포에서 뽑든 결과는 비슷하다. 어디서 뽑느냐가 중요한 것이 아닌 그 분포의 standard deviation이 얼마인지가 중요!

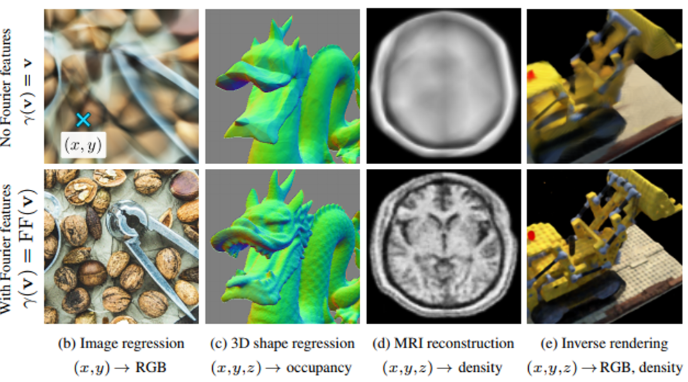
기존의 Coordinate-based MLPs가 low frequencies는 잘 학습하지만 high frequencies는 잘 학습하지 못하는 “spectral bias” 라는 현상을 Fourier features mapping을 통해 극복하고 이를 Neural Tangent Kernel 이론으로 설명한 논문
Coordinate-based MLPs가 spectral bias 문제를 겪는 이유는 급격한 주파수 감소를 가진 커널과 대응하기 때문이며 이를 Fourier features mapping을 통해 해결할 수 있다.