On this page
Denoising diffusion probabilistic models(2020)
PR-409 정리 내용
Intro
그동안은 Training 부분만 신경쓰고 Test 는 한번 하고 마는 접근방식이 많았는데 요즘은 Test 타임에서 이것저것 많이 하려고 하는 접근들이 성능, 퀄리티가 좋은 모습을 보여주는 추세로 보인다.
EX) RAFT
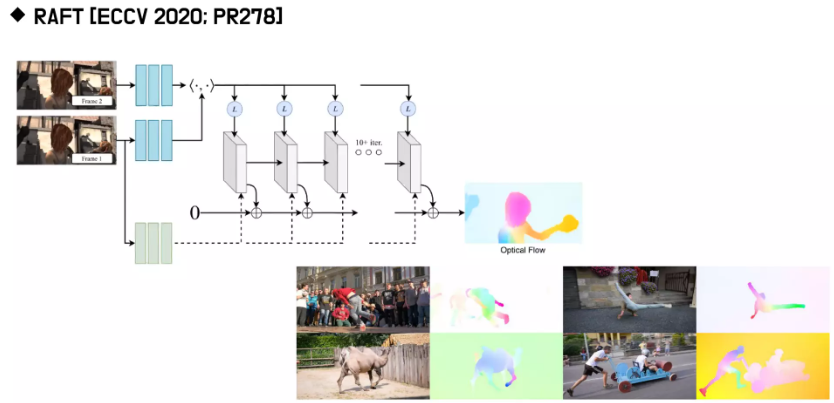
결과를 뽑고, 한번 더 뽑고, 한번 더 뽑고 하는 구조를 RNN 구조로 만들어서 Optical flow의 퀄리티를 개선해 나감
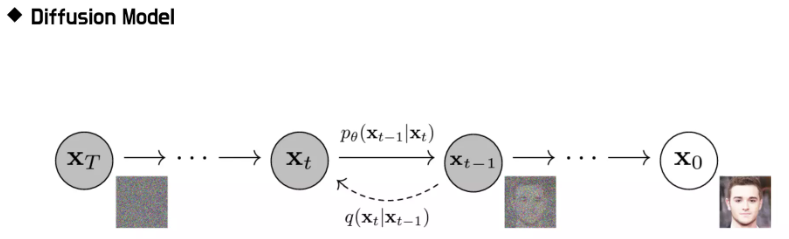
Diffusion 모델도 노이즈를 통해서 점점 개선이 되다가 원하는 이미지를 얻는 구조
RAFT와 비슷하게 iteration을 통해서 결과물을 얻는 알고리즘
Generative Models
생성 모델이 하고자 하는것 : “To know the distribution(manifold) of data”
예를 들어 MNIST 데이터가 있다고 하면, 28x28, \(28^2\) 인 벡터로 나타낼 수 있다.
그러면 \(28^2\) 차원의 공간에 무수히 많은 점을 찍을 수 있을텐데 MNIST 데이터는 \(28^2\) 차원보다는 낮은 차원의 특정한 스페이스를 따를 것 (그 안에만 있을 것이다 라는). 이것을 manifold라 하고 이 manifold를 찾자는 것
분포를 안다는 것은 데이터가 어떻게 생겼는 지를 아는 것
CelebA 데이터를 예시로 들면, 사람의 얼굴은 흔히 이렇게 생겼다더라 하는 정보를 네트워크가 학습을 하는 것
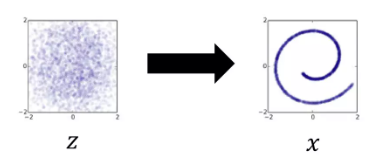
z에다가 f(z) 함수를 씌우면 x 가 나오는
z는 스페이스 상에 아무렇게나 찍은거니 정보가 적음
이 의미없는 점을 인풋으로 하는 함수를 학습 시켜서 이 함수가 내뱉는 아웃풋은 오른쪽 처럼 특정한 매니폴드 안에 있어서 의미가 있는, (information이 큰) 데이터를 얻게하는 함수를 학습시키자.
Supervised Learning이 아니기 때문에 Unsupervised하게 학습해야함 - loss 설계의 어려움
다른 생성모델로는
Variational Autoencoders
GANs
Normalizing Flow
가 있다.
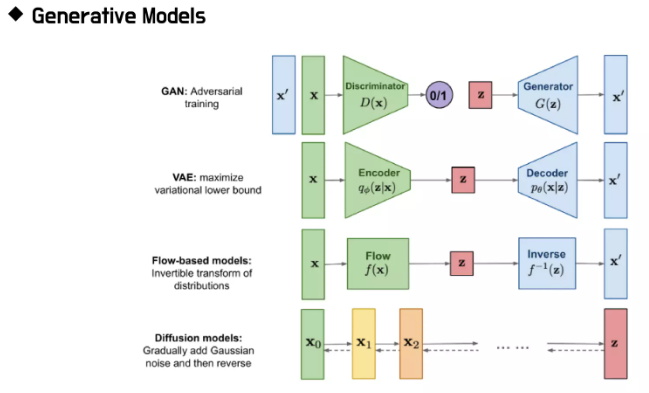
모델 별 diagram
Variational Auto Encoders
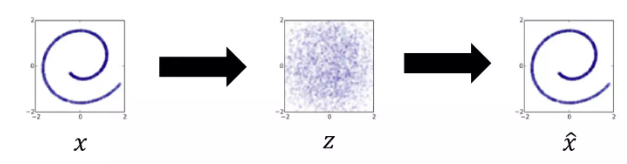
뒷부분 \(z \rightarrow \hat{x}\) 는 공통
어떤 함수 f(x)를 학습 시켜서 우리가 원하는 의미있는 x를 얻을 수 있는 함수를 얻고자하는 것.
전략: Reconstruction. 원본을 Encoding한 결과가 z이고 이를 다시 Reconstruction하도록 학습을 시켜보자
- 인코더를 추가했다는게 생성모델에서의 contribution.
Generative Adversarial Nets
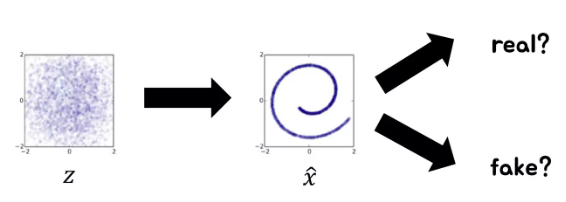
\(z \rightarrow \hat{x}\) 가 있는 것은 동일한데 인코더가 아니라 아웃풋에 대해서 discriminator를 정의해서 real인지 fake인지 구분하게 만들어 놓고 f(x)와 D를 경쟁시킨다.
Normalizing Flow Models
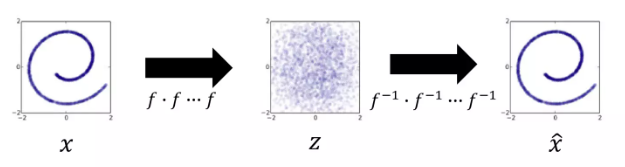
VAE와 인코더가 있다는 점은 비슷하지만 인코더가 inverse가 존재하는 함수들의 합성함수로 정의해놓고 디코더를 합성함수의 인버스로 정의
Diffusion Models
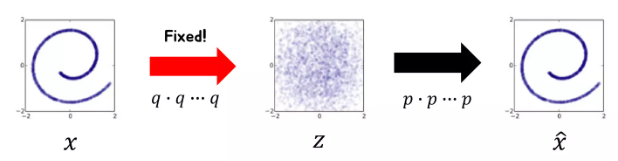
VAE, flow model과 비슷하지만, 인코더가 Fixed 되어있음! ← 핵심
VAE, flow model은 fixed되어있지 않고 joint하게 트레이닝이 된다.
사람이 설계한 인코딩 과정을 inverse하는 디코더만 학습을 시키자. 디퓨전 모델의 핵심 개념
Generative Models 정리 (장단점)
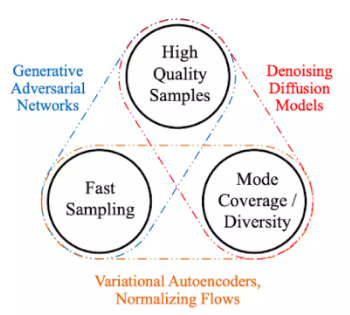
퀄리티가 좋아야하고 아웃풋의 다양성이 있어야 하며 샘플링이 빨라야한다.
Diffusion Probabilistic Models
Diffusion은 ICML 2015에서 처음 제안됨. (Deep unsupervised learning using nonequilibrium thermodynamics)
Diffusion?
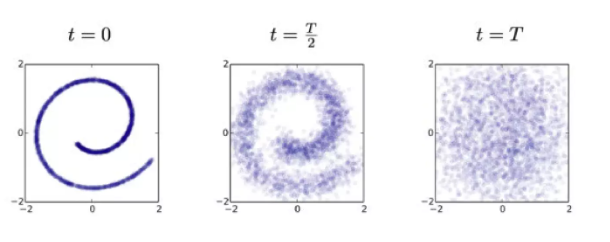
’확산’이라는 뜻 어떤 점들이 확산을 한다.
정보를 잃어가는 과정
열역학법칙에서도 우주가 정보를 점점 잃어가고 있다는 내용이 있다고 한다.
위 사진은 인코딩 과정. 의미가 있는 Manifold 위의 특정한 데이터들이 노이즈를 추가하면 추가할수록 공간 전체에 퍼져버려서 결국엔 아무 의미도 갖지 않는 노이즈 데이터로 변화해가는 모습을 디퓨전이라고 한다.
이걸 reverse하게 학습을 해서 의미가 있었던 시점으로 돌아가게끔 하고 싶은 것 ← 핵심
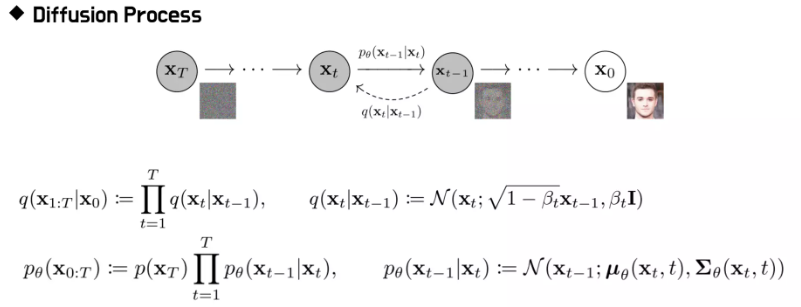
디퓨전은 여러번의 반복을 통해서 디퓨전이 일어난다.
노이즈를 한번에 더해버리면 문제가 너무 어렵기 때문에 적당한 노이즈를 조금씩 더해 나간다.
여기서 q가 forward diffusion(노이즈를 더해나가는 과정)
p가 inverse. (디퓨전을 한 노이즈를 되돌려서 우리가 원하는 이미지로 만드는)
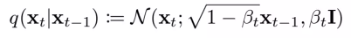
q는 다음과 같이 구성 (N은 Gaussian Noise, \(\sqrt{1-\beta_t}\bf{x}_{t-1}\) 이 mean, \(\beta_t \bf{I}\) 가 variance)
mean 부분을 보면 \(\beta\) 라는 파라미터가 있어서 베타에 따라 이전의 \(\bf{x}_{t-1}\) 에 있었던 정보들을 조금 지우고 그 부분에 노이즈를 주입
만약 \(\beta_t = 1\) 이면 mean이 0이 되면서 0을 mean으로 하고있는 Noise가 돼버림 → 한번에 이미지에서 노이즈로 점프를 하게 되는 것
\(\beta\) 가 작으면 작을수록 이미지가 변화가 없는 것이고 \(\beta\) 가 1에 가까울수록 이미지에 노이즈가 크게 들어가는 것
각 단계의 \(\beta\) 는 다 다른 값을 취하고 있다.
뒤에서 다룰 DDPM의 경우는 이 \(\beta\) 를 학습시키는 것이 아닌 fix를 한다.
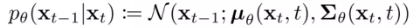
p는 결국 위의 노이즈 프로세스의 반대인 inverse process가 된다.
forward process가 가우시안이면 backward도 가우시안으로 모델링하면 된다는 증명이 있다고 한다.
이에 따라 가우시안으로 모델링
우리는 \(\mu_\theta(\bf{x}_t,t), \sum_\theta(\bf{x}_t, t)\) 를 예측을 해야하는 것
결국 \(\mu_\theta(\bf{x}_t,t)\) 가 예측의 결과가 되고 가우시안이 있는 이유는 확률적으로 대답을 하기 위함
p가 결국 우리가 알고싶어하는, 학습시키고자 하는 모델이고 q는 우리가 설정한 노이즈를 더해나가는 디퓨전 프로세스
p와 q 혼동 주의. 우리가 알고싶어하는건 inverse니까 p로 설정, forward가 q(우리가 설정한)

VAE에서 쓰고있는 Loss (ELBO?)
p랑 q를 VAE처럼 ELBO과정을 거쳐서 Loss를 구성함(Maximum Likelihood)
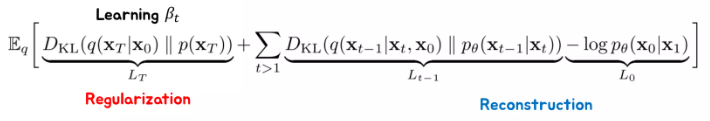
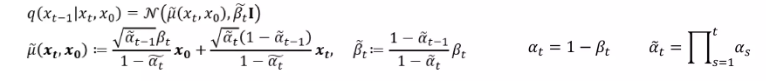
위 식은 결과만, 이 로스가 나온 계산과정은 추후에 다뤄보기
VAE의 loss처럼 Regularization term과 Reconstruction term이 하나씩 나온다.
Regularization term에서 p는 가우시안이고 q는 우리가 설정한건데 무엇을 학습하는 건지?
→ DDPM 이전에는 \(\beta_t\) 를 학습을 같이 해주었기 때문에 사용되었다.
Reconstruction term는 각 단계별로 노이즈를 잘 지우고 우리가 원하는 이미지를 잘 만들어내라 라는 term
\(L_{t-1}\) 은 노이즈를 점점 지워 나가는 프로세스에 대한 로스
\(L_0\) 은 이미지가 생성되기 직전 마지막 단계에서의 로스
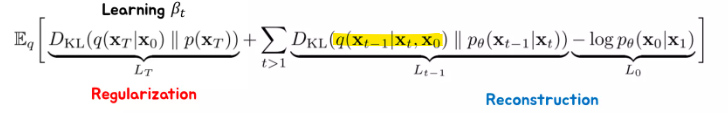
형광펜 부분 q에서, 분명히 \(\bf{x}_{t-1}\rightarrow \bf{x}_t\) 부분은 우리가 설정을 한다. (노이즈를 더하는)
근데 여기서는 q의 \(\bf{x}_t\) 로부터 \(\bf{x}_{t-1}\) 을 예측하는 부분이 나온다.
그럼 \(\bf{x}_t\) 로 부터 \(\bf{x}_{t-1}\) 을 구할 수 있는 q가 우리한테 주어지는 상황이면 p를 왜구하지? 라는 의문이 들 수 있다.
근데 여기서 \(\bf{x}_0\) 가 중요하다.
이 q는 \(\bf{x}_t\) 로 부터 \(\bf{x}_{t-1}\) 를 예측하거나 만들어 나가는 텀이 아니다. (디퓨전 프로세스의 역과정을 대표하기 위해 나와있는 텀)
원래 \(q(\bf{x}_t | \bf{x}_{t-1})\) 가 노이즈를 더해서 만드는 확률 분포인데 이걸 베이즈 같은걸로 뒤집으면 \(\bf{x}_{t-1}\) 로 부터 \(\bf{x}_{t}\) 로 가는 확률을 정의할 수 있을거고 그 과정에서 예측의 문제가 아니다 보니까 원본인 \(\bf{x}_0\) 가 같이 들어가게 된것
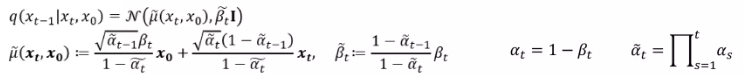
q에 대한 수식. 이 계산과정도 복잡하기에 결과만 다루고 과정은 추후에 다루기
최종 목적은 \(\bf{x}_0\) 이 주어지지 않아도 \(\bf{x}_t\) 를 잘 예측 하자라는게 목적이므로 KL Divergence가 그 목적을 잘 설명해주고 있는 것
Denoising Diffusion Probabilistic Modles (DDPM)
2015년 Diffusion Model에 이것저것 수정을 거친다.
Residual Estimation
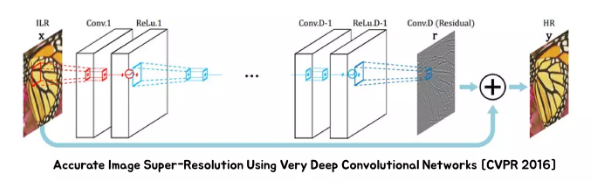
IDEA: low resolution 이미지가 high resolution 이미지가 가지고 있어야 할 대부분의 정보를 가지고 있는데 바로 예측하는 것은 아깝다. low resolution 이미지를 활용을 해보자!
- low resolution을 맨 뒤에 더해서 residual만 구해보자 (요즘은 residual만 구한다는 아이디어가 너무나 당연한 아이디어)
그런데 Diffusion은 이 당연한 아이디어를 사용하지 않고 있던 것.
\(\bf{x}_{t}\) 를 보고 \(\bf{x}_{t-1}\) 의 \(\mu\) 를 예측을 해야하는 건데 이 \(\mu\) 를 예측을 할 때 그냥 예측을 한 것
\(\mu_\theta\) 가 \(\bf{x}_t\) 와 굉장히 유사한 점이 많음에도 불구하고 그냥 예측을 한 것
그래서 결국 여기선 Residual만 예측을 하자는 것!
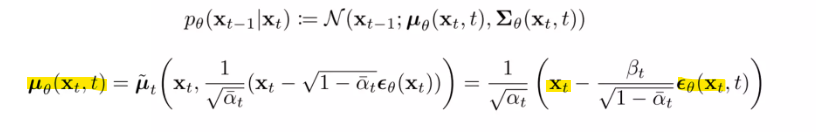
\(\mu_\theta\) 를 그냥 예측을 하는 것이 아니라 \(\epsilon_\theta\) 를 예측을 한 다음에 \(\bf{x}_t\) 에서 빼서 예측을 하자
그냥 예측하는 것이 아닌 레지듀얼을 예측하자는게 첫번째 아이디어
Loss Simplification
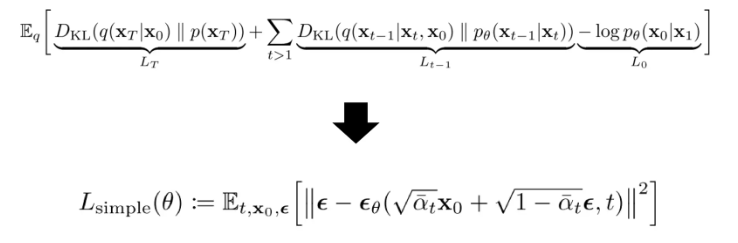
위가 원래 Diffusion Loss, 아래가 DDPM loss
아래를 보면, residual끼리 빼고 제곱을 하는 모습을 볼 수 있다.
Output과 GT 사이의 MSE를 구해서 이 로스를 줄이고자 하는 과정이 보니까 디노이징 알고리즘과 동일해서 논문 제목에 디노이징이 붙은 것
Loss Simplification #1 - Deleting Regularization Term
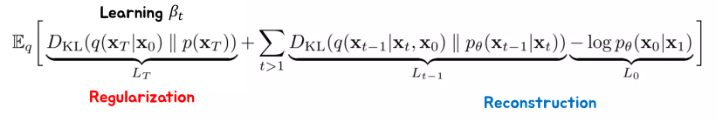
윗 식에서 Regularization Term을 보면, 이 텀은 \(\theta\) 에 관한 식이 아니다.
이는 단지 \(\beta_t\) 를 학습시키기 위한 term인데,
\(\beta_t\) 를 \(T=1000\) 기준으로 \(\beta_1 = 10^{-4} \quad \text{to} \quad \beta_T = 0.02\) 로 linear하게 설정하여 \(\beta_t\) 를 fix 해놓고 학습을 하니까 잘하더라 라는 것이 실험적으로 밝혀짐
→ 굳이 \(\beta_t\) 를 학습시킬 필요 없다!
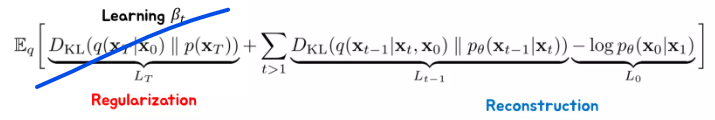
\(\beta_t\) 를 학습시킬 필요가 없기에 이 regularization term은 그냥 날려보내게 됨 (상수 값이 된다.)
뒤에도 마찬가지지만 inductive bias를 늘리는 방향으로 Contribution을 하게된다.
연구자가 설계한 부분들로 학습 가능한 부분들을 대체하자!
generative model이고 로스가 불안정하며 학습이 너무 어렵다 보니 인간의 사전지식을 투입하는 것

Loss Simplification #2 - Not to Learn Variance
- \(\beta_t\) 를 fix를 했으니 \(\beta_t\) 를 우리는 알고있는 상황.
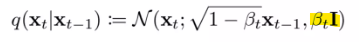
기존 모델의 variance를 보면, \(\beta_t\) 가 그대로 곱해져있는 형태이다.
즉, \(\beta_t\) 가 크면 클수록 노이즈가 클 것이고, 작으면 작을수록 노이즈가 작아질 것
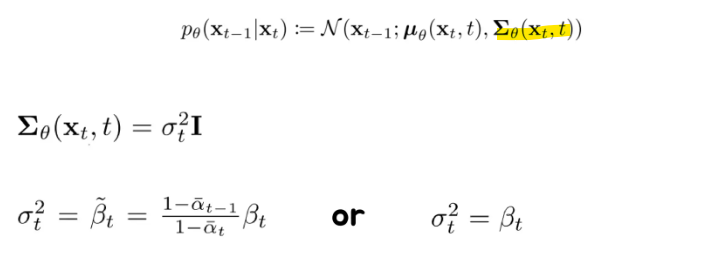
그러면 예측을 할 때 불확실성도 사실 \(\beta_t\) 로 부터 analytic 하게 구할 수 있지 않을까?
→ variance를 학습시킬 이유가 없어짐
그래서 아래 값으로 대체를 하자는 것!
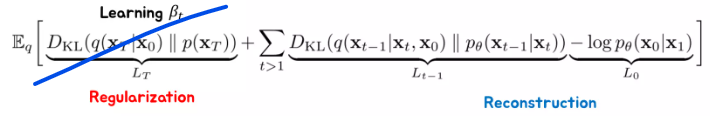
- 기존 loss

- 결국 \(L_{t-1}\) 을 이와 같이 \(\mu_\theta\) 로 인해 예측된 아웃풋이 GT에 가까워지도록 L2 loss를 주는 것과 같은 결과가 나오는 것
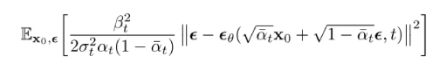
오른쪽의 \(\epsilon\) 관련 식을 대입을 하면 이와 같이 Simplification 된다.
앞부분은 상수니까 learning rate 같은걸로 포함되어 없애버리면
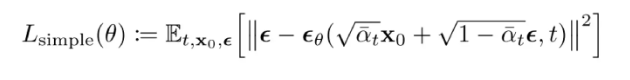
이와 같이 정리가 된다.
Experiments
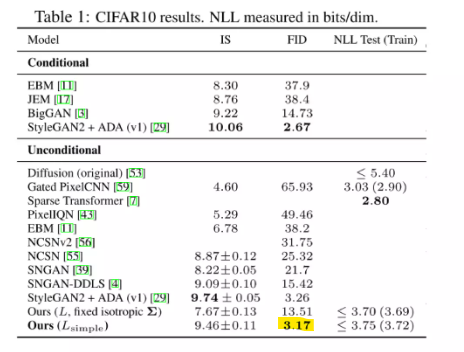
FID가 굉장히 좋음
generative model의 정량평가는 한계가 있으니 Visual Comparison을 확인해보면

- 굉장히 High Quality의 이미지를 얻을 수 있다.

- Noise로 부터 CIFAR-10의 이미지를 생성하는 과정을 보여주는 이미지