[Paper Review] Physics-informed neural network for lithium-ion battery degradation stable modeling and prognosis (2024)

On this page

• Physics-informed neural network for lithium-ion battery degradation stable modeling and prognosis
  • Research Objective
  • Research Motivation
  • Research Methodologies
  • Research Result
  • Conclusion

---

Physics-informed neural network for lithium-ion battery degradation stable modeling and prognosis

• Nature Communications

---

Research Objective

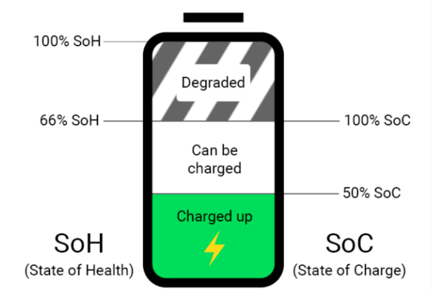
• 리튬이온 배터리의 state-of-health(SOH)를 정확하게 측정하는 것

  

Research Motivation

• Physics-based model:

  물리 기반 모델은 안정적이고 정확하지만, 화학적 구성이 다른 배터리의 경우 모델 매개변수가 다르고 계산 비용이 높다.

• Data-driven model:

  높은 정확도와 효율성을 가지고 있지만, 그 일반화 가능성은 추출된 특징에 의존하며 안정성이 낮다. (사용 조건의 높은 가변성으로 인해 기존 방법은 데이터셋 또는 작업 조건별로 특정 특징을 추출해야 하며, 이는 데이터셋 전용 모델로 이어져 컴퓨팅 리소스의 낭비를 초래)

→ PINN은 물리 기반 접근법과 데이터 기반 접근법의 강점을 결합하여 이러한 문제를 해결한다.

• 물리 정보를 고려함으로써 상대적으로 적은 데이터를 사용하여 모델을 훈련할 수 있다.

• 더 안정적이다.

- Physical knowledge + Machine learning 분류

• Sequential integration 방법: 물리 기반 모델과 머신러닝 모델이 독립적으로 존재, 별도의 단계에서 서로 연결되는 방식

  • A1: 물리 모델의 출력이 머신러닝 모델의 입력으로 사용되는 방식

  • A2: 물리 모델의 출력과 머신러닝 모델의 출력을 결합하여 최종 예측을 도출하는 방식. 이 경우, 두 모델의 예측 결과가 독립적으로 계산된 후 이를 합쳐서 최종 결과를 낸다.

  • A3: 머신러닝 모델의 출력이 물리 모델의 입력으로 사용되는 방식. 이는 물리 모델의 파라미터를 조정하거나 업데이트 하기 위해 머신러닝 모델의 예측 결과를 사용하는 경우에 해당

• Hybrid 방법: 물리 기반 모델과 머신러닝 모델을 하나의 프레임워크 안에 융합하는 방식으로, 보다 본질적으로 두 접근법을 통합. 이 방법들은 물리적 방정식을 직접 머신러닝 모델에 통합하여 학습하는 방식이다.

  • B1: 물리 모델을 엄격하게 제약 조건으로 사용하면서, 머신러닝 모델이 해당 제약 조건 내에서 작동하도록 한다. 예를 들어, 물리방정식이 신경망의 일부로 포함되어 학습과정에서 신경망이 물리적 제약을 따르도록 하는 방식

  • B2: 물리 방정식과 머신러닝 모델이 완전히 통합된 방식이다. 물리적 방정식과 머신러닝 모델이 단일 모델로 결합되어 동시에 학습되고, 물리 방정식이 데이터 기반 학습을 보완하거나 지원하는 역할이다.

  이 논문은 B2 아키텍쳐를 사용한다.(거버닝 방정식과 신경망을 통합하여 안정적이고 정확, 기존의 PINN 접근법과 달리, 배터리 화학 성분과 충전/방전 프로토콜이 다른 배터리 간 전이 학습 및 소규모 학습에서 그 발전을 검증)

Research Methodologies

Dataset

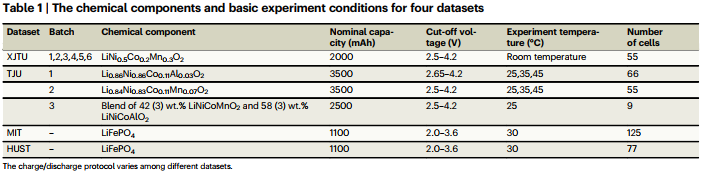
• 실험을 위해 4개의 대규모 공개 데이터셋 (총 387개의 배터리와 310,705개의 샘플을 사용)

• 이 데이터 셋은 XJTU, TJU, HUST, MIT 배터리 데이터셋으로 구성, 각 데이터 셋은 서로 다른 배터리 화학 성분과 충전/방전 프로토콜을 포함

- 특징 추출

• 목적: SOH 추정 성능을 향상시키기 위해 견고하고 일반화 가능한 특징을 추출하는 것이 중요

• 방법: 배터리가 완전히 충전되기 전 짧은 시간 동안의 데이터를 이용해 충전 전압 곡선과 전류 곡선에서 특징을 추출한다. 이 방법은 대부분의 배터리 데이터셋에서 일관된 특징을 추출할 수 있도록 설계한다.

  (완전히 방전되는 경우는 적지만 완전히 충전되는 경우는 많기에 ’충전’이 더 고정적이고 규칙적이다. 따라서 배터리가 완전히 충전되기 전의 짧은 기간의 데이터에서 특징을 추출한다.)

  

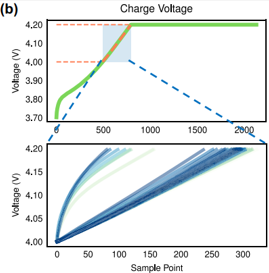
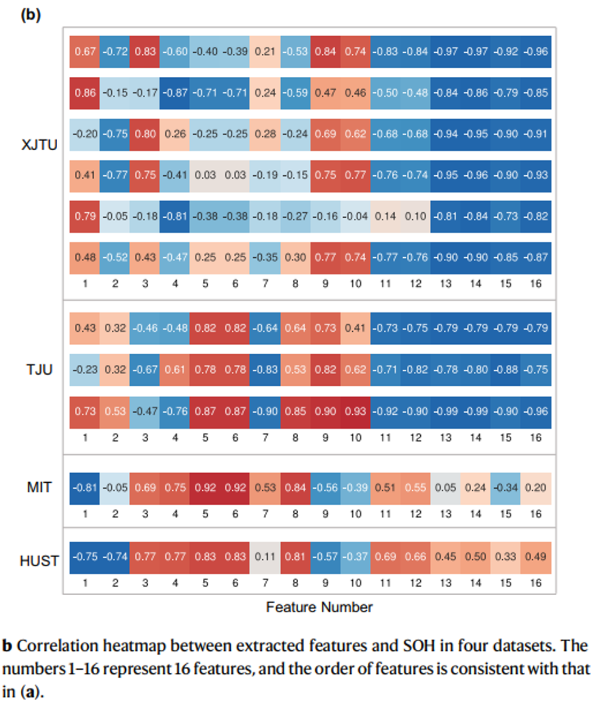
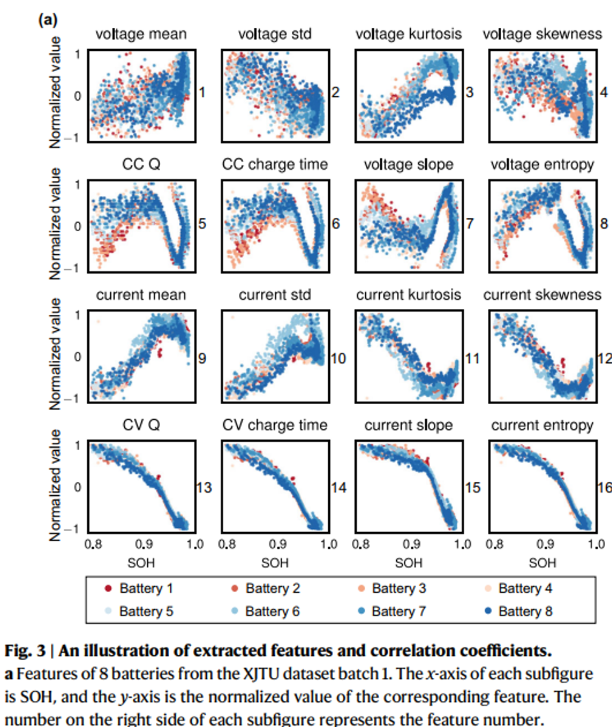
• 추출된 특징: 전압 및 전류의 평균값, 표준편차, 왜도, 첨도, 충전시간, 곡선 기울기, 곡선 엔트로피 등 16가지 특징 추출

• 상관관계 분석: 4개의 데이터셋(XJTU, TJU, MIT, HUST)에서 추출된 특징과 SOH 간의 피어슨 상관계수를 계산하여 배터리 화학 성분에 따라 상관관계가 다르게 나타남을 확인. 예를 들어 LiNiCo-x 계열 배터리(XJTU, TJU)의 경우, 특정 특징과 SOH간의 상관관계가 매우 유사했지만 LiFePO4 계열 배터리(MIT, HUST)에서는 다른 경향을 보였다.

  

  

---

1. 전기화학적 방정식의 복잡성을 고려하여, B2형 PINN 개발

• 경험적 열화 및 상태공간 방정식의 관점에서 배터리 열화 동역학 모델링, 신경망을 활용해 배터리 열화 동역학 포착

  

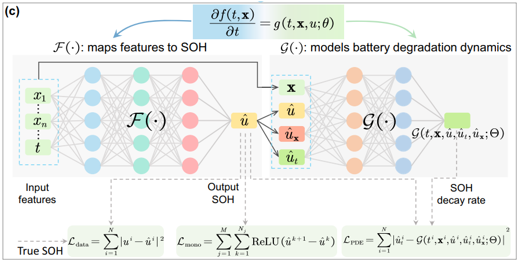
• 배터리 열화는 주로 가용 용량의 감소와 내부 저항의 증가로 나타나며, 이를 정확하게 설명하기 위해 여러 경험적 모델이 있으나 시간만을 독립 변수로 사용하는 단일 함수로 배터리 열화를 설명하는 것은 불충분하다. 이 연구에서는 배터리 열화를 다양한 변수(시간, 방전깊이(DOD), 충전률, 열화 지표 등)에 따라 다변수 함수로 모델링하는 접근법을 제안한다.

- PINN

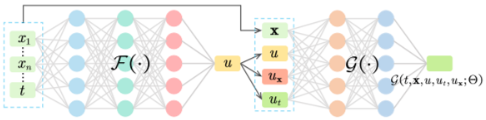
• F()는 SOH를 추정하는 역할을 하며, G()는 배터리 열화 동태를 모델링한다. 이 두 신경망은 배터리 상태를 예측하기 위해 함께 작동한다.

• G()함수의 명시적 형태를 알 수 없다는 문제를 해결하기 위해, PINN은 물리 기반 방정식과 신경망을 결합하여 G()의 근사치를 추정

• 손실함수: 모델 학습시 사용되는 손실함수는 데이터 손실, PDE 손실, 단조성 손실로 구성된다. 이 손실함수들은 모델이 배터리 열화 특성을 반영하고 정확한 SOH를 예측하도록 한다.

\[\mathcal{L}_{data}=\sum^N_{i=1}|u^i-\hat{u}^i|^2,\quad \mathcal{L}_{mono}=\sum^M_{j=1}\sum^{N_j}_{k=1}\text{ReLU}(\hat{u}^{k+1}-\hat{u}^k),\quad \mathcal{L}_{PDE}=\sum^N_{i=1}|\hat{u_t}^i - \mathcal{G}(t^i,\mathbf{x}^i,\hat{u}^i,\hat{u}_t^i,\hat{u}^i_{\mathbf{x}};\Theta)|^2\]

• 배터리 열화 모델링:

  \[u = f(t,\mathbf{x}) \quad \quad \cdots (1)\]

  여기서 \(u\) 는 SOH, t는 시간, \(\mathbf{x}\) 는 방전깊이(DOD), 충전 속도, 열화 지표 등 배터리 관련 변수

• SOH 변화율 방정식(시간에 따른 변화율):

  \[\frac{\partial u}{\partial t} = g(t,\mathbf{x},u;\theta) \quad \quad \cdots (2)\]

  여기서 g는 비선형함수, \(\theta\) 는 모델 구성 파라미터

  • 배터리의 상태가 시간에 따라 어떻게 변하는 지를 의미

  • 하지만 g(.)의 명시적인 형태를 알기 어렵고 표현력이 부족 → feature를 늘려 근사

  \[u_t = \frac{\partial u}{\partial t} \approx g'(t,\mathbf{x}, u, u_t, u_\mathbf{x}, u_\mathbf{xx}, ... ; \theta') \quad \quad \cdots (3)\]

  • 여기서 학습 가능한 파라미터 \(\Phi\) 를 사용하여 \(f(t,\mathbf{x})\) 를 모델링하는데 신경망 \(\mathcal{F}(t,\mathbf{x}; \Phi)\) 를 사용한다. 이후 automatic differentiation mechanism을 활용하여 \(u_t\) 와 \(u_\mathbf{x} = [\frac{\partial u}{\partial x_1}, \frac{\partial u}{\partial x_2}, ...]^T\) 를 계산한다.

    \(u_\mathbf{x}\) 는 1차 편미분이고, \(u_\mathbf{xx}\) 는 2차 편미분을 나타낸다.

    이 접근 방법의 한 가지 장점은 g(.)에 대한 후보 기저 함수 집합을 지정할 필요가 없고, 대신 보다 일반화된 근사 함수 g’(.)를 사용한다는 점이다. 함수 근사값 g’(.)는 t, u, x 및 그 임의 차수 부분 도함수에 대해 보다 유연한 관계를 제안한다.

    학습 가능한 파라미터 \(\Theta\) 를 가진 신경망 \(\mathcal{G}(.)\) 를 사용하여 g’(.)를 모델링하면 주어진 x, t 및 기타 부분 도함수로부터 배터리의 노화 매커니즘을 학습할 수 있다.

    정확도와 계산 복잡성의 균형을 맞추기 위해 1차 부분 도함수의 영향만 고려하기로 하고 고차 도함수는 제외한다.

    앞서 언급한 분석을 기반으로 PINN \(\mathcal{H}\) 를 정의한다. 이 식 (4)는 식 (2)와 (3)으로 부터 유도된다.

    \[\mathcal{H}:=\frac{\partial \mathcal{F}(t, \mathbf{x}; \Phi)}{\partial t} - \mathcal{G}(t,\mathbf{x}, u, u_t, u_\mathbf{x};\Theta) \quad \quad \cdots (4)\]

    여기서 \(\frac{\partial \mathcal{F}(t, \mathbf{x}; \Phi)}{\partial t}\) 는 t에 대한 솔루션 신경망 \(\mathcal{F}(.)\) 의 t에 대한 미분을 나타내며 \(\mathcal{G}(.)\) 는 신경망으로 모델링한 배터리 열화 동적 방정식을 나타낸다.

    

• SOH 계산 방정식: 배터리의 특정 충전 사이클 \(k\) 에서의 SOH \(u^k = f(t_k, x_k) = \frac{Q^k}{Q^0}\)

  • 여기서 \(Q^k\) 는 사이클 \(k\) 에서의 배터리 용량을, \(Q^0\) 는 초기 용량을 나타낸다. 이 방정식은 배터리의 현재 용량을 초기 용량과 비교하여 SOH를 계산하는 방식이다.

    SOH 값 \(u^k\) 는 t=k 일 때 degradation trajetory \(f(.)\) 의 한 지점과 일치한다.

    \(u_t\) 를 근사화 하려면 샘플 지점 i 에서 \(\mathcal{H}(t^i, \mathbf{x}^i) = 0\) 이 유지되도록 해야 한다.

    따라서 PINN의 최적화 프로세스는

    \[\mathcal{L}_{PDE} = \sum^N_{i=1} |\mathcal{H}(t^i, \mathbf{x}^i)|^2\]

    를 준수해야 한다.

• 한 페이지로 정리하면 다음과 같다.

---

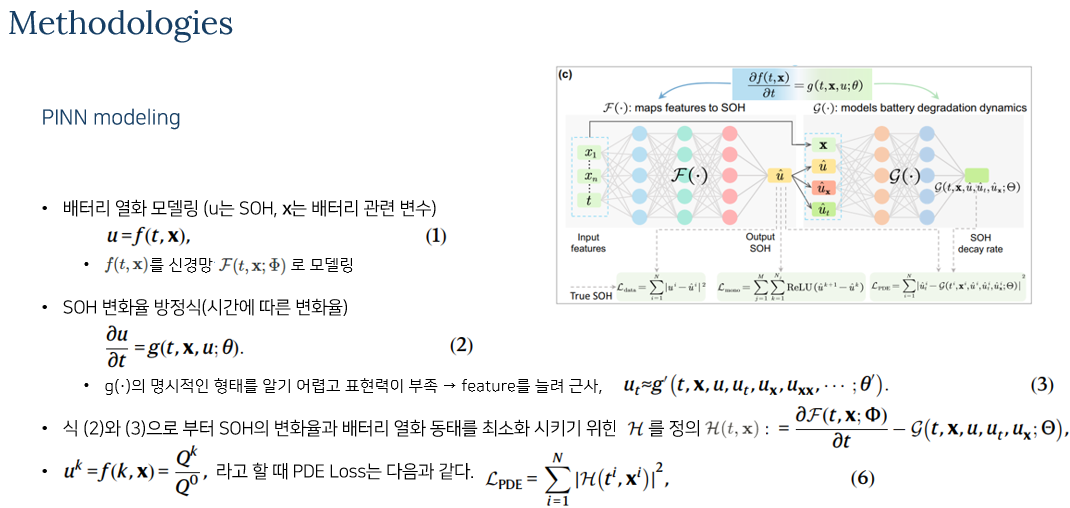
• PDE 손실함수: PINN의 학습과정에서 사용되는 손실 함수는 다음과 같이 정의된다.

  \[\mathcal{L}_{PDE} = \sum^N_{i=1}||\frac{\partial u^i}{\partial t} - g(t^i, x^i, u^i, u^i_x, u^i_t;\theta)||^2\]

  • 여기서 \(N\) 은 샘플 수를 나타내며 각 샘플에 대해 SOH 변화율과 실제 g 함수 값 사이의 차이를 최소화 하는 방식으로 모델이 학습된다. 이 손실 함수는 모델이 배터리의 열화 동태를 정확하게 학습할 수 있도록 돕는다.

• 데이터 손실 함수: 실제 데이터와 모델 예측 값 사이의 오차를 최소화하기 위해

  \[\mathcal{L}_{data} = \sum^N_{i=1}|u^i - \hat{u}^i|^2\]

  • 여기서 \(u^i\) 는 실제 SOH 값이고 \(\hat{u}^i\) 는 모델이 예측한 SOH 값이다. 이 손실 함수는 모델이 실제 데이터에 맞게 조정되도록 돕는다.

• 단조성 손실 함수: 배터리의 SOH는 시간이 지남에 따라 감소해야 한다는 물리적 제약을 반영하기 위해 단조성 손실 함수가 추가

  \[\mathcal{L}_{mono} = \sum^{M-1}_{j=1}\text{ReLU} (\hat{u}^{j+1}-\hat{u}^j)\]

  \(\hat{u}^j+1\) 와 \(\hat{u}^j\) 는 각각 연속된 두 사이클에서의 예측 SOH 값이다. 이 함수는 예측 값이 연속된 사이클에서 감소하도록 강제하여, 배터리의 자연스러운 열화 과정을 반영한다.

• 전체 손실 함수

  \[\mathcal{L} = \mathcal{L}_{data}+\alpha\mathcal{L}_{PDE}+\beta\mathcal{L}_{mono}\]

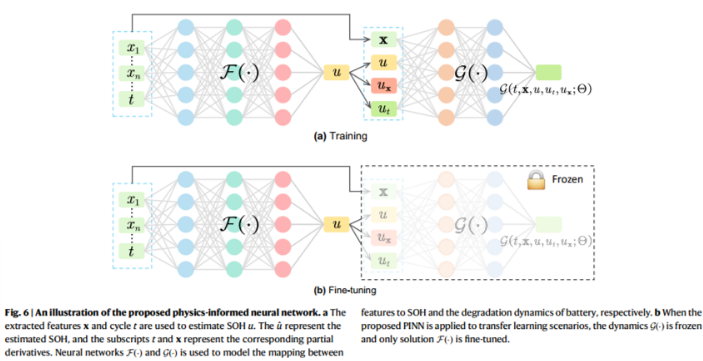
1. Training

• PINN은 입력 특징(전압, 전류 등)과 사이클 수를 사용하여 SOH를 추정한다.

• 함수 F()는 SOH 추정을 담당하며 G()는 배터리 열화 동태를 모델링한다. 두 함수 모두 신경망으로 구성되며 학습단계에서는 이 두가지를 모두 훈련한다.

2. Fine-tuning

• 전이학습시 G()는 고정(frozen)되고, 오직 F()만 미세조정한다.

• 이 방법은 이미 학습된 배터리 열화 동태를 기반으로 새로운 데이터에 맞게 모델을 조정하는 데 사용된다. 이는 다른 충전/방전 프로토콜과 데이터셋 간의 전이 학습에서 유용하게 작동한다.

• G()는 충전/방전 프로토콜 및 데이터 세트와 무관하며 F()는 이들과 관련이 있기 때문에 F()만 미세 조정하고 G()의 가중치는 동결한다.

---

Research Result

- SOH 추정 (SOH Estimation)

• 추정 방법: 추출된 16개 특징과 시간(사이클 수)이 PINN의 입력으로 사용되어 SOH를 추정. 특징 크기의 차이가 모델에 미치는 영향을 줄이기 위해 모든 특징에 대해 min-max normalization 수행

• 결과: PINN의 SOH 추정 성능을 기존의 MLP, CNN과 비교. 그 결과 PINN이 더 나은 성능을 보였으며, 특히 안정성이 뛰어났다.

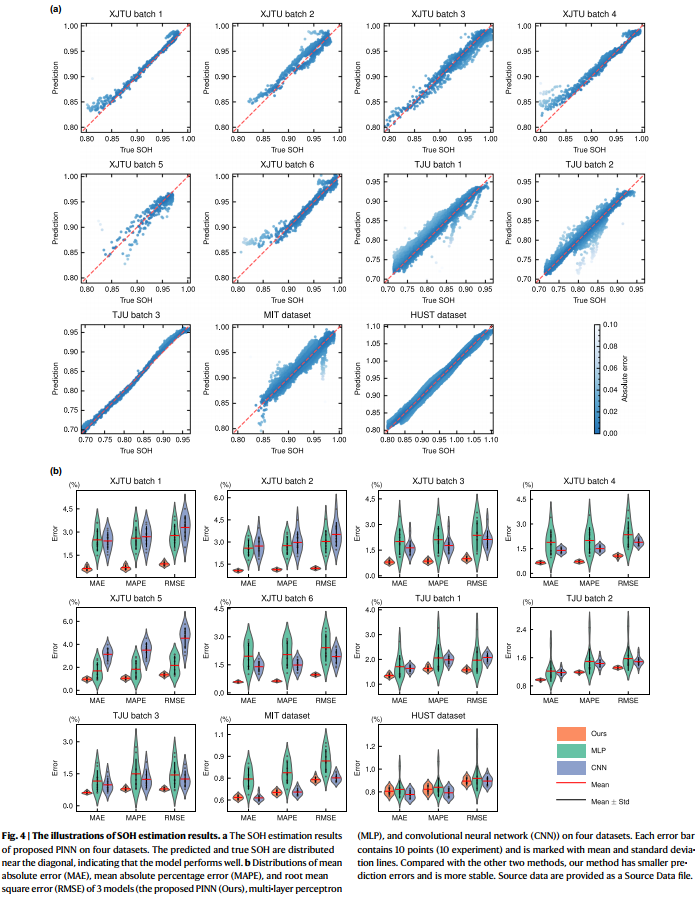
(a): SOH 추정 결과 (scatter plots)

(b): SOH 추정 오차 분포 (Violin plots): MAPE에서 특출난 효과

- 소규모 샘플 실험

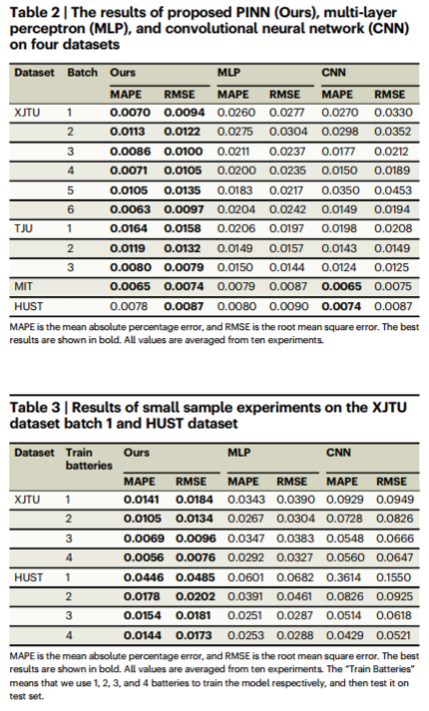
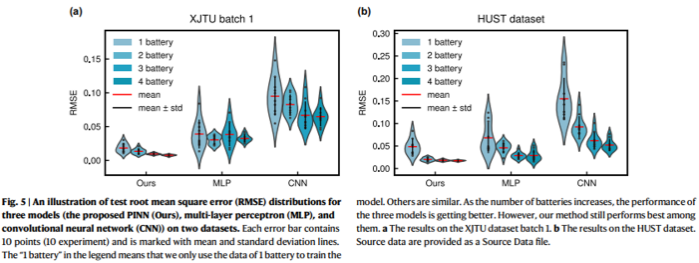
• 제안된 PINN 모델은 4가지 데이터셋과 소규모 샘플 실험 모두에서 MLP와 CNN에 비해 우수한 성능을 보여준다.

• 특히 데이터가 적을 때도 높은 예측 정확도와 안정성을 유지하는 것이 특징이다. 이는 소규모 데이터셋을 사용하는 상황에서도 유용하게 적용될 수 있음을 시사한다.

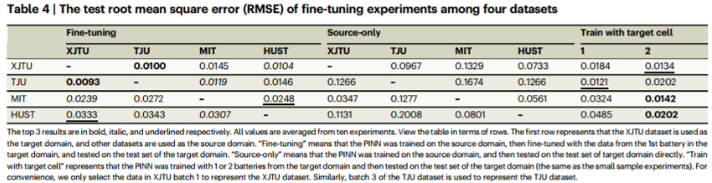
• 전이학습 실험에서 얻은 RMSE 값

• 전이 학습을 통해 모델은 새로운 데이터셋에서 성능을 높일 수 있으며, 특히 배터리 열화 동태를 잘 포착하여 다른 화학 성분의 배터리에도 적용할 수 있다는 점을 강조한다. 이는 PINN이 다양한 상황에서 SOH를 정확하게 추정할 수 있음을 보여준다.

• 추가적으로 XJTU 데이터 세트와 TJU 데이터 세트는 모두 LiNiCo-x 배터리이며, 특징과 SOH 간의 상관관계가 더 유사하므로 이들 간의 미세 조정 효과가 더 좋다.

• 마찬가지로 MIT와 HUST는 모두 LiFePO \(_4\) 배터리이며, 이들 간의 미세 조정 효과도 유망하다. 이는 의미 있는 발견일 수 있다.

Conclusion

• 이 논문에서는 PINN의 잠재력을 강조하며, 이 방법이 배터리 SOH추정과 열화 모델링에 있어 중요한 도구가 될 수 있음을 시사한다. PINN은 물리 기반 모델과 데이터 기반 모델의 장점을 결합하여 보다 정확하고 일반화 가능한 배터리 상태 예측을 가능하게 한다.