On this page
Introduction to Optimum Design
1. Introduction to Design Optimization
시스템의 설계는 최적화 문제로 정식화될 수 있으며 여기서는 모든 제약조건(constraint)을 만족하면서 기능의 척도를 최적화하게 된다.
Design은 iterative. 계속 바뀌어나가고 업데이트한다.
1.1 설계 과정
Preliminary Design: 시스템 레벨, 큰 그림, 이전의 디자인들 반영
Detail Design: 서브 시스템 레벨, 세부적, 잘게 쪼갬
proto type이나 test는 선택사항. (위험도 기준으로?)
1.2 공학설계와 공학해석
Analysis: 주어진 역학문제, 이미 만들어진 문제 푸는 것. (closed problem)
Design: 만들어 나가는 것. To calculate shape/size. (open problem)
Design을 위해 analysis가 필요하다.
벤치마킹 → 설계 → analysis
1.3 전통적 설계과정과 최적설계과정
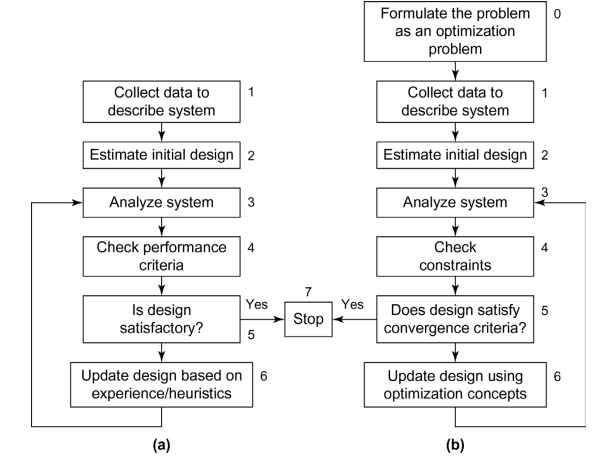
- 전통적 설계과정, (b) 최적설계과정
0.최적 설계과정에는 0단계가 있다. 여기에서 최적화 문제가 정식화된다. 목적함수도 여기에서 정의된다.
4.전통적 설계과정은 성능 기준의 만족 여부를 점검하고, 최적설계과정에서는 1단계에서 정식화된 제약조건의 만족 여부를 점검한다.
6.전통적 설계과정은 설계자의 경험이나 직관 및 이전의 서계에서 얻은 정보에 의존하고, 최적설계과정에서는 최적화의 개념이나 과정을 이용한다.
1.4 최적설계와 최적제어
1.5 기본 용어와 표현
1.5.1 벡터와 점
1.5.2 집합
1.5.3 제약조건의 표현
1.5.4 상첨자/하첨자와 합의 표현
1.5.5 벡터의 노름/크기
1.5.6 다변수함수
- 이 책의 전반에 걸쳐 모든 함수는 연속(continuous)이며 최소한 두 번 미분가능(twice-differentiable)하다고 가정한다.
1.5.7 함수의 편도함수
1계 편도함수
n변수함수 \(f(x)\) 에 대한 1계 편도함수는 다음과 같다.
\[\frac{\partial f(\mathbf{x})}{\partial x_i};\quad i=1 \ \text{to} \ n\]
위 식의 n개의 편도함수를 보통 열벡터로 정렬하고, 이를 함수 \(f(x)\) 의 경사도(gradient)라고 하며 다음과 같이 표기한다.
\[ \nabla f(\mathbf{x}) = \frac{\partial f(\mathbf{x})}{\partial \mathbf{x}} = \begin{bmatrix} \frac{\partial f(\mathbf{x})}{\partial x_1} \\ \frac{\partial f(\mathbf{x})}{\partial x_2} \\ \vdots \\ \frac{\partial f(\mathbf{x})}{\partial x_n} \end{bmatrix}\]
위의 2개 식에서 경사도의 성분은 벡터 \(\mathbf{x}\) 의 함수이다.
2계 편도함수
위의 식의 경사도 벡터의 성분을 다시 미분하여 함수 \(f(\mathbf{x})\) 의 2계 도함수를 얻는다.
\[\frac{\partial^2 f(\mathbf{x})}{\partial x_i \partial x_j}; \ i, \ j=1 \ \text{to} \ n\]
위의 식에는 \(n^2\) 개의 편도함수가 있다. 이들을 행렬로 배열할 수 있으며 이를 헷세행렬(Hessian matrix)이라고 한다. 헷세행렬은 \(\mathbf{H(x)}\) 또는 함수 \(f(x)\) 의 2계 편도함수 행렬이라 하고, 다음과 같이 표기한다.
\[\mathbf{H}(\mathbf{x}) = \nabla^2 f(\mathbf{x}) = \begin{bmatrix} \frac{\partial^2 f(\mathbf{x})}{\partial x_i \partial x_j} \end{bmatrix}_{n \times n}\]
함수 \(f(x)\) 가 2회 연속 미분가능하면 위 식의 헷세행렬 \(\mathbf{H(x)}\) 는 대칭행렬이다.
벡터함수의 편도함수
\[\mathbf{g}(\mathbf{x}) = \begin{bmatrix} g_1(\mathbf{x}) \\ g_2(\mathbf{x}) \\ \vdots \\ g_m(\mathbf{x}) \end{bmatrix} = \begin{bmatrix} g_1(\mathbf{x}) & g_2(\mathbf{x}) & \dots & g_m(\mathbf{x}) \end{bmatrix}^T\]
벡터함수 \(\mathbf{g(x)}\) 를 미분하여 얻은 경사도 벡터들은 \(n \times m\) 매트릭스가 된다. 이를 벡터함수 \(\mathbf{g(x)}\) 의 경사도 행렬(gradient matrix)이라 하고 다음과 같이 표기한다.
\[\nabla \mathbf{g}(\mathbf{x}) = \frac{\partial \mathbf{g}(\mathbf{x})}{\partial \mathbf{x}} = \begin{bmatrix} \nabla g_1(\mathbf{x}) & \nabla g_2(\mathbf{x}) & \dots & \nabla g_m(\mathbf{x}) \end{bmatrix}_{n \times m}\]
경사도 행렬은 보통 행렬 \(\mathbf{A}\) 라고 표기한다.
\[ \mathbf{A} = \begin{bmatrix} a_{ij} \end{bmatrix}_{n \times m}, \quad a_{ij} = \frac{\partial g_j}{\partial x_i}, \quad i = 1 \text{ to } n, \, j = 1 \text{ to } m \]
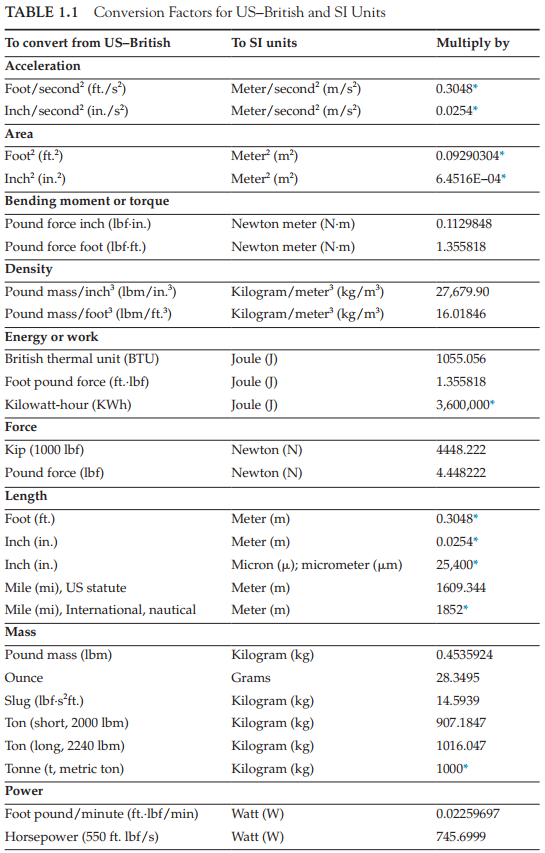
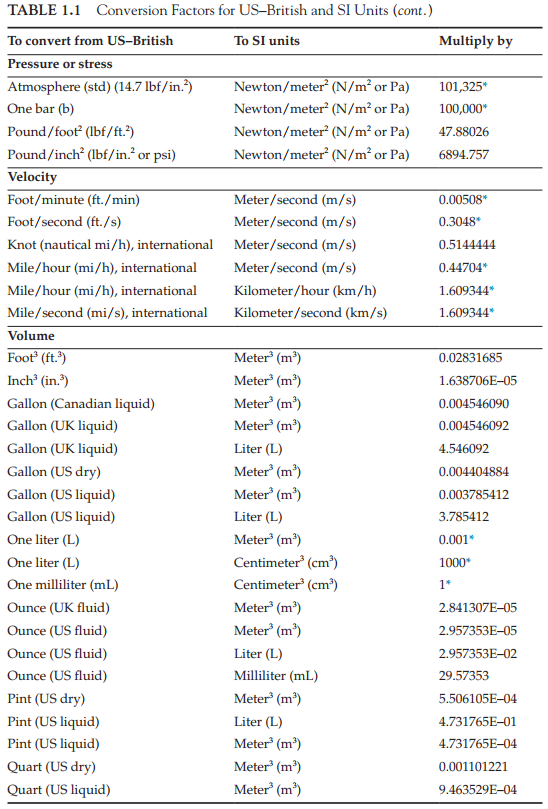
1.5.8 영미 단위계와 국제표준단위계
설계문제의 정식화에 대한 개념이나 과정 및 최적화 방법들은 계량의 단위와는 무관하다.
따라서 문제를 정의하는 데 어떤 단위를 쓰는가 하는 것은 관계없지만 수식의 표현은 사용단위에 따라 달라진다.
이 책에서는 영미 단위와 국제표준단위(SI unit)를 예제와 연습문제에서 사용할 것이므로 이 단위들은 알아두어야 한다.
하나의 단위계에서 다른 단위계로 변환하는 것은 비교적 간단하다.
영미단위와 SI 단위 사이의 변환에는 표1.1의 변환상수를 이용하면 편리하다. 표에는 흔히 사용되는 양에 대한 변환상수가 수록되어 있으며 좀 더 완전한 표는 IEEE/ASTM (2010) 발간물을 참고하면 된다.