On this page
Introduction to Optimum Design
2. Optimum Design Problem Formulation
- Formulation(정식화)
- 이 장의 주요내용:
설계문제의 서술문을 최적화를 위한 수학적 표현으로의 변환
문제의 설계변수 확인 및 정의
최적화 목적함수의 확인 및 정의
설계 제약조건의 확인 및 정의
정식화된 설계문제를 설계최적화의 표준 모형으로 변환
어떤 문제의 정확한 정식화에 소요되는 노력은 그 문제를 풀기 위한 전체 노력의 약 50%정도가 필요
대부분의 설계최적화 문제는 다음과 같이 5단계를 통하여 정식화된다.
1단계: 과제/문제 설정
2단계: 자료 및 정보 수집
3단계: 설계변수 정의
4단계: 최적화 기준 정의
5단계: 제약조건 정의
최적설계문제의 정식화는 서술형 문장으로 표현된 문제를 잘 정리된 수학적 표현으로 변환하는 것이다.
2.1 문제 정식화 과정
2.1.1 1단계: 과제/문제 설정
2.1.2 2단계: 자료 및 정보 수집
2.1.3 3단계: 설계변수 정의
2.1.4 4단계: 최적화 기준 정의
2.1.5 5단계: 제약조건 정의
2.2 캔 설계
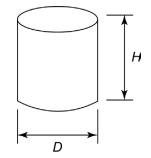
Volume \(V\) must be at least 400mL (1mL = 1 \(\text{cm}^3\))
\(3.5 \le D \le 8\), cm
\(8 \le H \le 18\), cm
cost of metal sheet: \(\$0.008/cm^2\)
Build a can with minimum cost
mathematical formulation
- 원하는 것? objective function
objective function
\[f(D,H) = [\pi DH+ 2(\frac{\pi}{4}D^2)] \times 0.008\]
(옆면, 위 아래 넓이)
Constraints 제약조건
\(\frac{\pi}{4}D^2 H \ge 400 cm^3\)
\(3.5 \le D \le 8\), cm
\(8 \le H \le 18\), cm
- 만약 constraint가 없으면? unconstrained problem.
…
2.11 최적설계의 일반적 수학 모형 General mathematical model
표준설계최적화 모형(standard design optimization model): 등호 및 부등호제약조건하에서 목적함수를 최소화하는 것
- 최적화에 관한 문헌에서는 이를 비선형계획문제(nonlinear programming problem)라고도 한다.
2.11.1 표준설계최적화 모형
\(\text{minimize}_x \ f(x)\)
\(\text{subject to}\ g_i(x)\le 0,\quad i=1,...,m\)
\(\ \ \quad \quad \quad \quad h_j(x)=0, \quad j=1,...,p\)
\(f(x)\) 를 최소화 하는 \(x\)를 찾아라.
\(f(x)\) : objective function, cost function, loss function
\(x\) : design variable \(\quad x = \{x_1, ..., x_n\} \quad\), \(n\) : # of design variables
\(g_i(x)\le 0 \leftarrow\) inequality constraints, \(\quad i=1,...,m \leftarrow\) # of inequality constraints
\(h_j(x)=0 \leftarrow\) equality constraints, \(\quad j=1,...,p \leftarrow\) # of equality constraints
2.11.2 최대화 문제
\(F(x)\) 를 최대화 하는 것은 \(f(x)=-F(x)\) 를 최소화하는 문제로 변환할 수 있다.
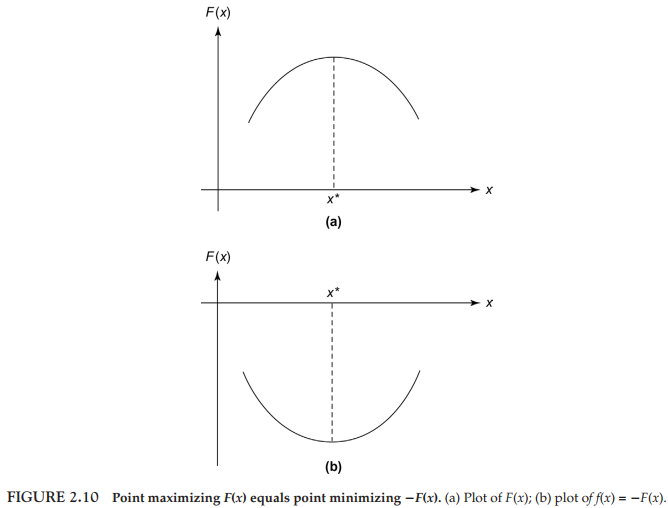
\(F(x)\)는 점 \(x^*\) 에서 최대인데, 보다시피 \(f(x)\) 는 동일점 \(x^*\) (\(F(x)\) 가 최대인 점)에서 최소치를 가진다. 그러므로 \(f(x)\) 를 최소화하는 것은 \(F(x)\) 를 최대화 하는 것과 동등하다.
2.11.3 “이상형(\(\ge\))” 제약 조건
표준설계최적화 모형에서는 “\(\le\)형” 부등호제약조건만을 취급하게 되어 있다.
\(g_i\le 0 \Leftrightarrow G_i(x) \ge 0\) when \(G_i(x)=-g(x)\)
2.11.5 표준 모형에 관한 고찰
2.등호제약조건의 개수: 상호 독립적인 등호제약조건의 수는 설계변수의 수보다 적거나 기껏해야 같아야 한다. 즉, \(p\le n.\)
\(p<n\) : the optimal solution is possible
\(p=n\) : no optimal solution is necessary (exact solution을 구할 수 있다)
\(p>n\) : redundant constraints should be deleted(잉여 제약조건을 제거) or no solution(해가 \(\infty\))
3.부등호제약조건의 개수: 부등호제약조건의 개수에 대한 제한은 없다.
- 그러나 최적해에서 등호로서 만족되는 활성제약조건(active constraint)의 수는 보통 설계변수의 개수보다 적거나 같다.
4.비제약 최적화 문제: 어떤 설계문제에서는 제약조건이 전혀 없을 수도 있다. 이러한 문제를 비제약 최적화문제(unconstrained optimization problem)라 하며 다른 것들은 제약 최적화문제(constrained optimization problem)라 한다.
5.선형계획문제: 모든 함수 \(f(x), h_j(x), g_i(x)\)가 설계변수의 선형함수이면 이러한 문제를 선형계획문제(linear programming problem)라고 한다.
이들 중 어느 함수라도 비선형이면 비선형계획문제(nonlinear programming problem)라 한다.
linear 하면 superposition이다. superposition = additivity(\(f(x_1+x_2)=f(x_1)+f(x_2)\)) + scaling(\(f(\alpha x) = \alpha f(x)\))
6.함수의 스케일링(scaling): 목적함수에 양의 상수를 곱해도 최적설계(최적해)가 변하지 않는다. 단지 최적의 목적함수 값만이 변한다. 또한 목적함수에 임의의 상수를 더하여도 최적설계에는 영향을 미치지 않는다.
마찬가지로 부등호제약조건에는 임의의 양의 상수를 곱해도 상관 없으며 등호제약조건에는 어떤 상수를 곱해도 된다. 이렇게 하여도 유용영역에 영향을 미치지 않으며 따라서 최적해에도 영향을 주지 않는다.
그러나 이상의 모든 변환이 후에 정의되는 라그랑지 승수(Lagrange multipliers)의 값에는 영향을 미치게 되며 이에 관한 것은 4장에 예시될 것이다. 또한 수치해법의 성능은 이들 변화에 의해 영향을 받는다.
+ \(\text{minimize}_x\ f(x) \Leftrightarrow \text{minimize}_x\ af(x)\)
\(\quad \quad \quad \quad \quad \quad \quad \ \ \ \Leftrightarrow \text{minimize}_x [f(x)+C]\)
where \(a\) is the positive constant
두 경우 다 optimal solution은 바뀌지 않는다.
2.11.6 유용집합(feasible set)
유용집합(feasible set): 모든 유용설계의 집합
제약집합(constraint set)과 유용설계영역(feasible design space)이라는 용어는 설계의 유용집합을 표현하기 위해 사용된다.
문자 \(S\)를 제약집합을 나타내는 기호로 사용하면, 수학적으로 \(S\)는 모든 제약조건을 만족하는 점(설계)의 집합이다:
\[S = (\mathbf{x}|h_j(\mathbf{x})=0, j=1\ \text{to}\ p; g_i(\mathbf{x})\le 0, i=1\ \text{to}\ m)\]
- 설계모형에 제약조건이 부가되면 유용영역은 보통 축소되며, 몇 개의 제약조건을 제거하면 유용영역은 확장된다.
2.11.7 활성/만족/위배제약조건
부등호제약조건 \(g_i(\mathbf{x}) \le 0\)이 등호로서 만족할 때, 즉 \(g_i(\mathbf{x}^*) = 0\)일 때, 이를 설계점 \(\mathbf{x}^*\)에서 활성제약조건이라 한다. (엄격제약조건 또는 구속(binding)제약조건이라고도 한다.)
부등호제약조건은 활성제약조건일 수도 있고 그렇지 않을 수도 있다.
그러나 등호제약조건은 모두 유용설계에 대하여 활성제약조건이다.
만족제약조건
위배제약조건
2.11.8 이산형과 정수형 설계변수
2.11.9 최적화 문제의 유형
2.12 실용적 문제의 정식화
Note that optimization problems from different fields of engineering can be transcribed into the standard model.