On this page
Maximum Likelihood Estimation(MLE)
정리 내용입니다.
우도는
모델이 데이터와 잘 맞을수록 커지고, 추정치가 데이터와 잘 맞을수록 커진다.
즉, 모델과 추정치가 데이터와 잘 맞으면, 데이터를 잘 설명하면 높아지는 값
모델과 추정치가 데이터와 잘 맞는 정도를 확률로 표현한 것.
최우추정치: 데이터에 가장 잘 맞는 추정치
최대우도법: 데이터에 가장 잘 맞는 모델과 추정치를 계산하는 방법
우도와 확률의 차이?
모델, 추정치 → 데이터
- 확률은 모델과 추정치가 원인이고 데이터가 결과
데이터 → 모델, 추정치
- 우도는 데이터가 원인이고 모델과 추정치가 결과
ex) 모델과 추정치가 이럴 때, 이 데이터가 나올 ‘확률’
ex) 데이터가 어떤식으로 찍혀있을 때 이 모델과 추정치가 잘 맞을 ’우도’는 얼마인가?
데이터로부터 모델을 추정!!!
최대우도법 정의
최대우도법(Maximum Likelihood Estimation, 이하 MLE)은 모수적인 데이터 밀도 추정 방법으로써
파라미터 \(\theta=(\theta_1,...,\theta_m)\) 으로 구성된
어떤 모르는 확률밀도함수 \(P(x|\theta)\) 에서 관측된
표본 데이터 집합을 \(x=(x_1,x_2,...,x_n)\) 이라 할 때,
이 표본들에서 파라미터 \(\theta=(\theta_1,...,\theta_m)\) 를 추정하는 방법이다.
Example
다음과 같이 5개의 데이터를 얻었다고 가정하자.
\(x=\{1,4,5,6,9\}\)
이 때, 아래의 그림을 봤을 때 데이터 \(x\)는 주황색 곡선과 파란색 곡선 중 어떤 곡선으로부터 추출되었을 확률이 더 높을까?
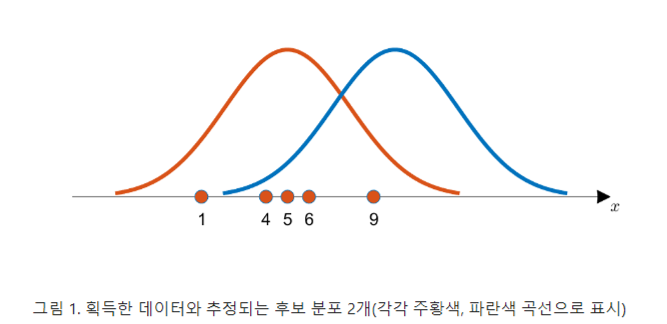
눈으로 보기에도 파란색 곡선 보다는 주황색 곡선에서 이 데이터들을 얻었을 가능성이 더 커보인다. 왜냐면 획득한 데이터들의 분포가 주황색 곡선의 중심에 더 일치하는 것 처럼 보이기 때문이다.
이 예시를 보면, 우리가 데이터를 관찰함으로써 이 데이터가 추출되었을 것으로 생각되는 분포의 특성을 추정할 수 있음을 알 수 있다. 여기서는 추출된 분포가 정규분포라고 가정했고, 우리는 분포의 특성 중 평균을 추정하려고 했다.
Likelihood function
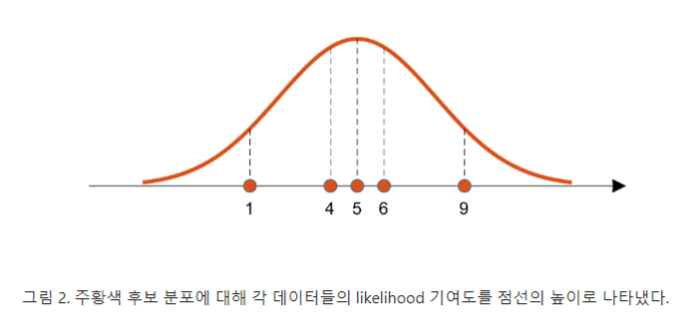
likelihood라는 것은 지금 얻은 데이터가 이 분포로부터 나왔을 가능도를 말한다.
수치적으로 이 가능도를 계산하기 위해서는 각 데이터 샘플에서 후보 분포에 대한 높이(즉, likelihood 기여도)를 계산해서 다 곱한 것을 이용할 수 있을 것이다.
계산된 높이를 더해주지 않고 곱해주는 것은 모든 데이터들의 추출이 독립적으로 연달아 일어나는 사건이기 때문.
그렇게 해서 계산된 가능도를 생각해볼 수 있는 모든 후보군에 대해 계산하고 이것을 비교하면 우리는 지금 얻은 데이터를 가장 잘 설명할 수 있는 확률분포를 얻어낼 수 있게 된다.
수식으로 써보면,
전체 표본 집합의 결합밀도 함수를 likelihood function이라고 한다.
\[P(x|\theta)=\prod^n_{k=1}P(x_k|\theta)\]
위 식의 결과 값이 가장 커지는 \(\theta\)를 추정값 \(\hat{\theta}\)로 보는 것이 가장 그럴듯하다.
보통은 자연로그를 이용해 아래와 같이 log-likelihood function \(L(\theta|x)\)를 이용한다.
\[L(\theta|x)=\text{log}P(x|\theta)=\sum^n_{i=1}\text{log}P(x_i|\theta)\]
? \(L(x|\theta)\) 가 아닌 \(L(\theta|x)\) 인 이유?
로그 우도 함수의 목적
특정한 데이터 \(x\) 가 주어졌을 때, 그 데이터가 나올 가능성을 최대화하는 파라미터 \(\theta\) 를 찾는 것.
표기법 \(L(\theta|x)\)
여기서 \(L(\theta|x)\) 이라는 표기는 주어진 데이터 \(x\) 가 있을 때 파라미터 \(\theta\) 에 의존하는 함수라는 의미. 즉, “데이터 \(x\) 가 주어졌을 때, \(\theta\) 에 대한 로그우도” 를 나타낸다.
데이터 \(x\) 를 고정한 상태에서 파라미터 \(\theta\) 에 의존하는 함수. 우리가 관심있는 변수(파라미터 \(\theta\) )를 강조하기 위해 사용
Likelihood function의 최대값을 찾는 방법
결국 Maximum Likelihood Estimation은 Likelihood 함수의 최대값을 찾는 방법이라 할 수 있다.
log 함수는 단조증가 함수이기 때문에 likelihood function의 최대값을 찾으나 log-likelihood function의 최대값을 찾으나 두 경우 모두 최대값을 갖게 해주는 정의역의 함수 입력값은 동일하다.
따라서 보통은 계산의 편의를 위해 log-likelihood의 최대값을 찾는다.
어떤 함수의 최대값을 찾는 방법 중 가장 보편적인 방법은 미분계수를 이용하는 것이다.
즉, 찾고자하는 파라미터 \(\theta\)에 대하여 다음과 같이 편미분하고 그 값이 0이 되도록 하는 \(\theta\)를 찾는 과정을 통해 likelihood 함수를 최대화 시켜줄 수 있는 \(\theta\)를 찾을 수 있다.
\[\frac{\partial}{\partial \theta}L(\theta|x)=\frac{\partial}{\partial \theta}\text{log}P(x|\theta)=\sum^n_{i=1}\frac{\partial}{\partial \theta}\text{log}P(x_i|\theta)=0\]
MLE의 조금 더 복잡한 예시(모평균, 모분산 추정)
평균 \(\mu\) 와 분산 \(\sigma^2\) 를 모르는 정규분포에서 표본 \(x_1, x_2, ..., x_n\) 을 추출했을 때, 이들 값을 이용해서 모분포의 평균과 분산을 추정해보자. 표본을 위와 같이 추출하였다고 하면
모평균의 추정값은
\[\hat{\mu} = \frac{1}{n}\sum^n_{i=1}x_i\]
모분산의 추정값은
\[\hat{\sigma}^2 = \frac{1}{n}\sum^n_{i=1} (x_i-\mu)^2\]
이다. 이것을 최대우도법을 이용해서 확인해보면,
각각의 표본들은 정규분포에서 추출된다고 했을 때 각 표본의 표본분포는
\[f_{\mu, \sigma^2}(x_i) = \frac{1}{\sigma \sqrt{2\pi}}\text{exp}(-\frac{(x_i-\mu)^2}{2\sigma^2})\]
이고, \(x_1, x_2, ..., x_n\) 은 모두 독립적으로 추출했다고 가정하자. 그러면 우도(likelihood)는
\[P(x|\theta) = \prod^n_{i=1}f_{\mu, \sigma^2}(x_i) = \prod^n_{i=1}\frac{1}{\sigma\sqrt{2\pi}}\text{exp}(-\frac{(x_i-\mu)^2}{2\sigma^2})\]
이고, 로그-우도는
\[L(\theta|x) = \sum^n_{i=1}\text{log}\frac{1}{\sigma\sqrt{2\pi}}\text{exp}(-\frac{(x_i-\mu)^2}{2\sigma^2})\]
\[= \sum^n_{i=1}\{\text{log}(\text{exp}(-\frac{(x_i-\mu)^2}{2\sigma^2})-\text{log}(\sigma\sqrt{2\pi})\}\]
\[=\sum^n_{i=1}\{-\frac{(x_i-\mu)^2}{2\sigma^2}-\text{log}(\sigma)-\text{log}(\sqrt{2\pi})\}\]
이다. 따라서 \(L(\theta|x)\) 를 \(\mu\) 에 대해 편미분하면,
\[\frac{\partial L(\theta|x)}{\partial \mu} = -\frac{1}{2\sigma ^2} \sum^n_{i=1}\frac{\partial}{\partial \mu} (x_i^2 - 2x_i \mu + \mu^2)\]
\[= -\frac{1}{2\sigma^2}\sum^n_{i=1}(-2x_i+2\mu)\]
\[=\frac{1}{\sigma^2} \sum^n_{i=1} (x_i-\mu) = \frac{1}{\sigma^2}(\sum^n_{i=1} x_i - n \mu) = 0\]
따라서, 최대우도를 만들어주는 모평균의 추정량은
\[\hat{\mu} = \frac{1}{n}\sum^n_{i=1} x_i\]
이다.
한편, \(L(\theta|x)\) 를 표준편차 \(\sigma\) 로 편미분하면
\[\frac{\partial L(\theta|x)}{\partial \sigma} = -\frac{n}{\sigma} - \frac{1}{2}\sum^n_{i=1}(x_i-\mu)^2 \frac{\partial}{\partial \sigma}(\frac{1}{\sigma^2})\]
\[=-\frac{n}{\sigma} + \frac{1}{\sigma^3}\sum^n_{i=1}(x_i-\mu)^2 = 0\]
따라서, 최대우도를 만들어주는 모분산의 추정량은
\[\hat{\sigma}^2 = \frac{1}{n} \sum ^n _{i=1} (x_i - \mu)^2\]
이라는 것을 알 수 있다.