On this page
End-to-End Optimized Image Compression(2017)
PR-328 정리 내용
Image Compression
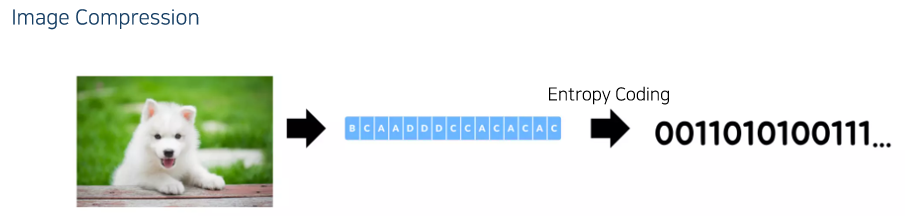
Image Compression은 이미지를 어떠한 시퀀스로 바꾼 뒤 이를 엔트로피 코딩 하는 과정
시퀀스로 바꾸는 방법에는 Lossless Coding과 Lossy Coding이 있다.
Lossless Coding은 원본 그대로 복원이 가능하다. (bmp)
Lossy Coding은 이미지를 조금 훼손시키더라도 엔트로피를 더 줄여보자는 방법. (JPEG)
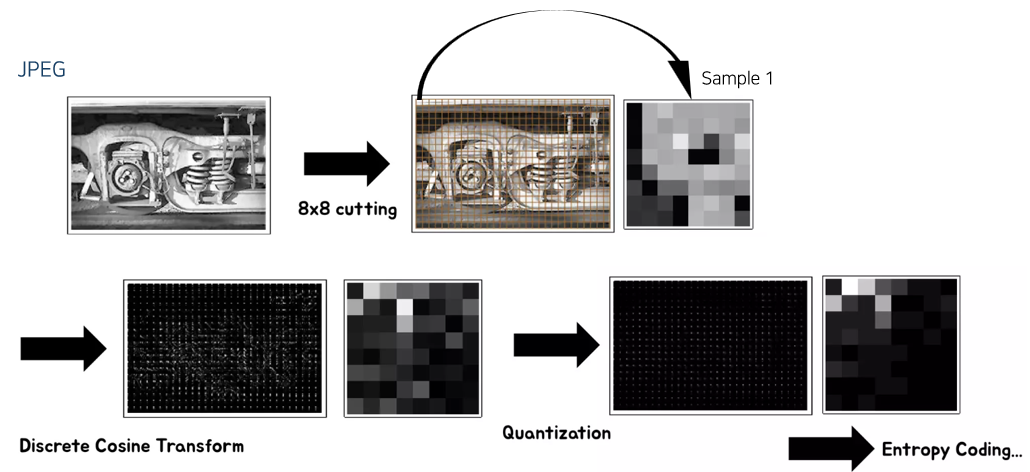
이 논문의 제안 방법이 JPEG 방법을 거의 그대로 사용하여 살펴보겠다.
과정은 8x8 픽셀로 cutting을 하고, Discrete Cosine Transform을 한 뒤 Quantization 과정 후 Entropy Coding을 하게 된다.
샘플 1개(8x8)는 앞에서 본 시퀀스의 A, B 등 알파벳에 해당한다.
Discrete Cosine Transform은 Fourier Trnasform의 Real 버전이라고 생각하면 되고, Linear Transform이다.
Frequency domain으로 바꾼 다음에 나온 값들을 quantization을 통해 sparse하게 만든다. Ex) 0 ~ 10 → 0, 5, 10
이후 Entropy Coding을 수행한다. (0, 5, 10에 대한 확률 값을 얻을 수 있으니 비트를 할당 가능하다.)

왼쪽이 Lossless, 오른쪽이 Lossy
JPEG 같은 Lossy Coding은 원본을 완벽하게 복원할 수 없다. (Quantization 과정에서 정보 손실)
이 과정에서 엔트로피를 줄였지만 퀄리티도 줄어들었다.
Lossless는 퀄리티가 좋지만 그만큼 엔트로피도 크고, 그에 따라 비트레이트도 크다.
Lossy는 반대로 퀄리티는 낮지만 그만큼 엔트로피도 작아지고, 비트레이트도 더 줄일 수 있다.
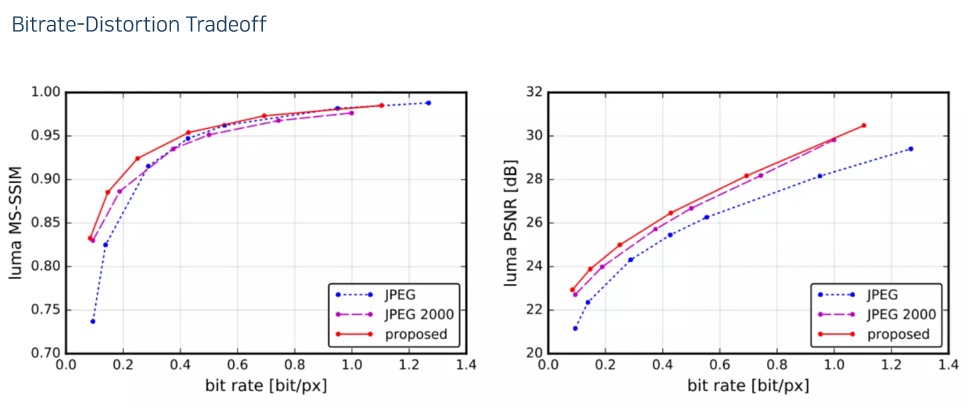
- 비트레이트가 높으면 성능이 좋고, 비트레이트가 낮으면 성능이 나쁘다. 왼쪽 위에 있을수록 좋은 방법
End-to-End Optimized Image Compression [Network Structure]
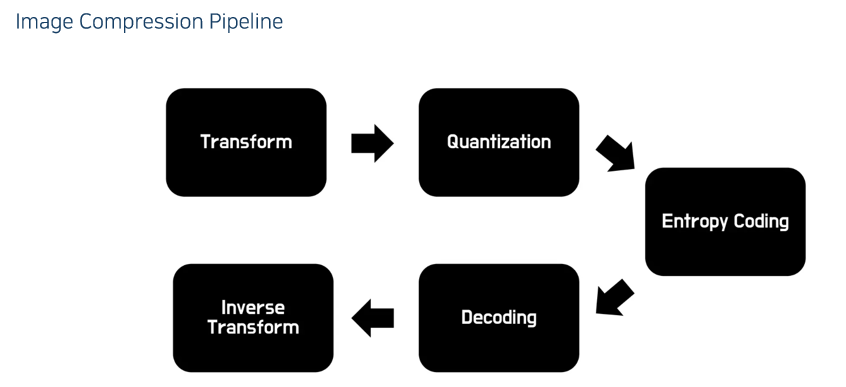
이미지 압축은 대부분 이러한 파이프라인을 가진다.
- Transform은 JPEG의 경우 DCT.
Entropy Coding 까지가 인코딩, 이후가 디코딩
Quantization을 했기에 Input과는 다른 결과가 나오게 될 것.
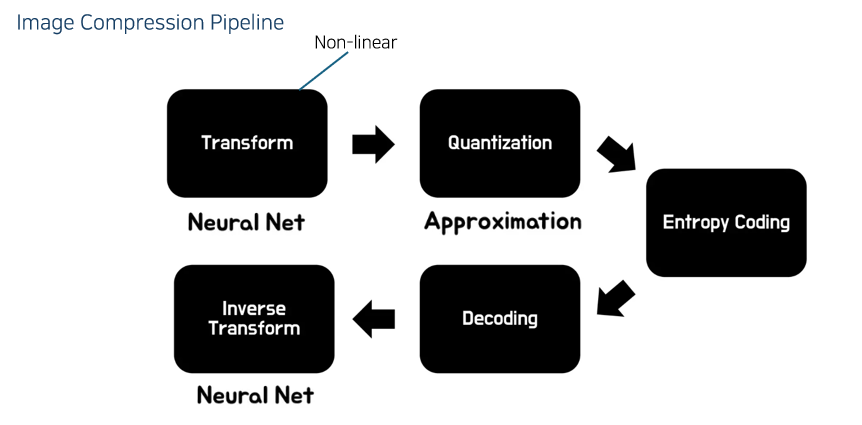
이 논문도 이 파이프라인을 그대로 따른다.
Transform은 뉴럴넷으로 대체를 하였다. (non-linear)
Quantization은 그대로 한다. 다만 Quantization은 값이 계단 처럼 나오기에 대부분의 미분값이 0이다. 이를 해결하기 위해 근사치를 사용한다.
Entropy Coding과 Decoding은 고정
Inverse Transform도 뉴럴넷으로 시킨다. 실제로 역함수 관계는 아니지만 둘 사이의 MSE를 설정해서 End-to-End로 학습을 하기에 서로가 Inverse 형태가 되도록 자연스럽게 학습이 될 것.

수식 순서대로 Convolution, Pooling(Downsampling), Activation 역할
GDN은 따로 관련 논문이 있다고 한다.
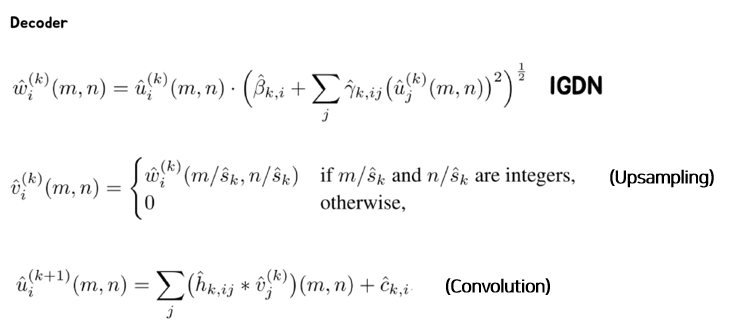
뉴럴넷이다 보니 완벽한 Inverse는 존재할 수 없지만, 구조라도 inverse하게 설계해보았다고 한다.
맨 위 식을 보면, 인코더의 마지막 수식의 분모를 그대로 가져다 곱한 모습을 볼 수 있다.
그 다음 Pooling의 반대 연산인 Upsampling을 하였다. 조금 다른 것은 중간중간 값을 Bilinear interpolation 등을 하는게 아니라 0으로 채우고,
이후에 아래 식에서 볼 수 있듯 컨볼루션 연산을 한다.
인코더와 디코더가 정반대의 연산 flow를 가진다.
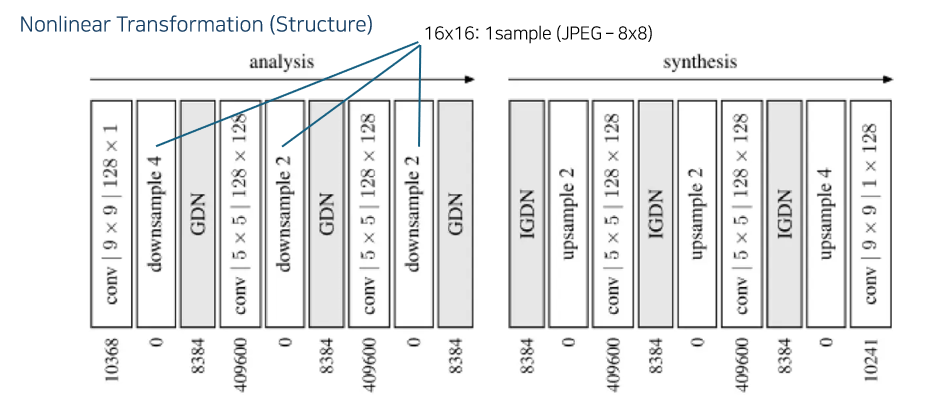
구조를 보면 다음과 같은데, 여기서 같은 구조가 3번씩 반복이 된다.
1/4, 1/2, 1/2로 다운샘플링 하기에 16x16의 패치를 하나의 샘플로 보겠다는 것이다.
즉, JPEG보다 더 큰 영역을 샘플 하나로 표시하려고 하는 것이기에 더 많이 압축을 할 수 있을 것이다.
End-to-End Optimized Image Compression [Optimization]
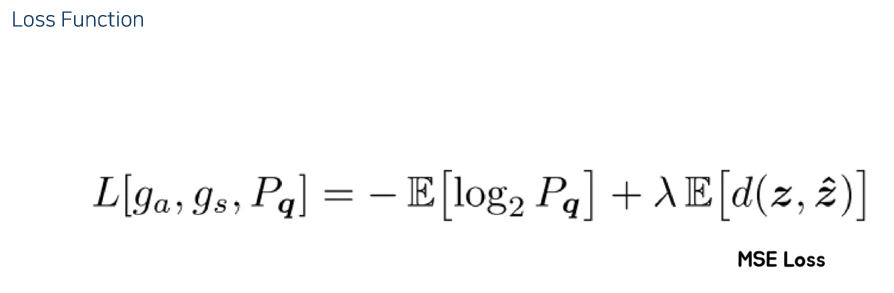
- Optimization 부분을 한번 보면, Loss function은 뒷부분은 MSE Loss이고, 앞부분은 Rate Loss → Entropy를 줄이라는 loss이다.
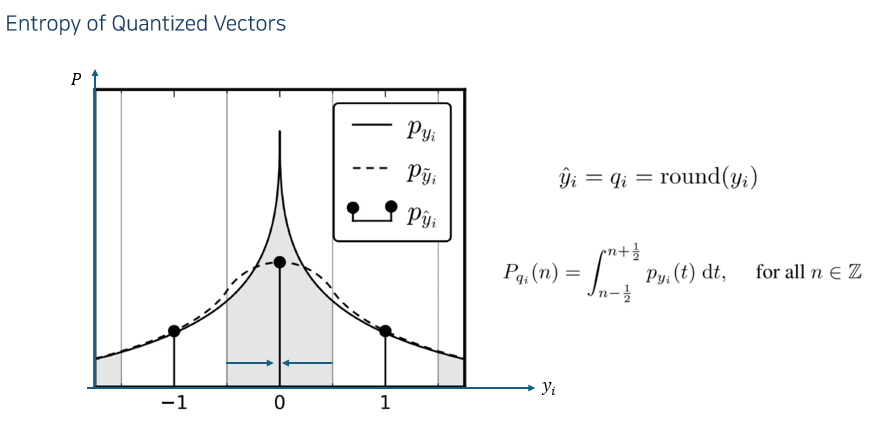
\(\hat{y}\) 을 quantized vector 라고 하자. (y의 round 값)
가로축이 \(y_i\) 의 값, 세로축이 probability density 라고 할 때,
뾰족한 실선이 실제 \(y_i\) 의 distribution이라고 하면 반올림을 했기 때문에, 적분을 하면 quantized된 벡터의 Probability Mass Function을 구할 수 있을 것이다.
그러면 이 PMF 값으로 엔트로피를 구할 수 있다.
그러나 앞에서 보았듯 Quantization의 결과는 training하기 어렵다. (미분하면 대부분 0)
그래서 \(\hat{y}\) 를 \(\tilde{y}\) 로 근사한다.
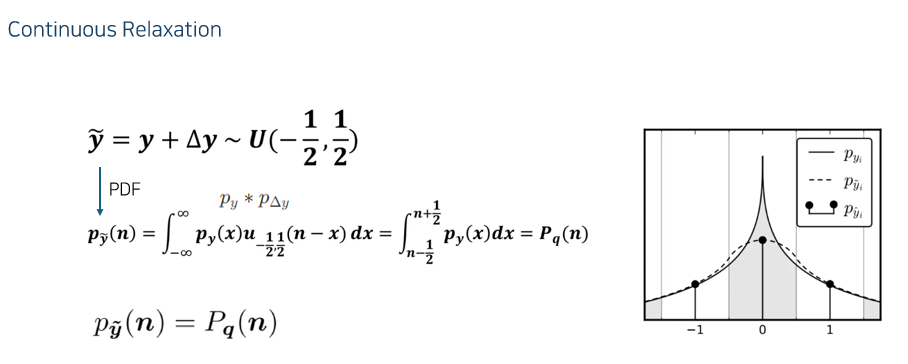
예를 들어, \(\hat{y}\) 이 0이라는 값이 나왔을 때 \(y\) 가 어디에 있었을까를 생각해보면 -1/2 ~ 1/2 사이의 값일 것이다.
이를 수식적으로 나타낸 값이 \(y+\Delta y\)
\(\Delta y\) 는 -1/2 ~ 1/2의 값을 가지는 random variable이다. (노이즈를 더하는 느낌)
\(\tilde{y}\) 는 continuous 하니까 pdf를 구할 수 있을 것이다. (여기서 점선이 \(\tilde{y}\) 의 그래프)
r.v. A와 r.v. B가 있을 때 r.v C = A+B 라고 하면, C의 pdf는 A의 pdf와 B의 pdf의 컨볼루션이다.

- \(\tilde{y}\) 를 적용한 Loss function은 다음과 같다.
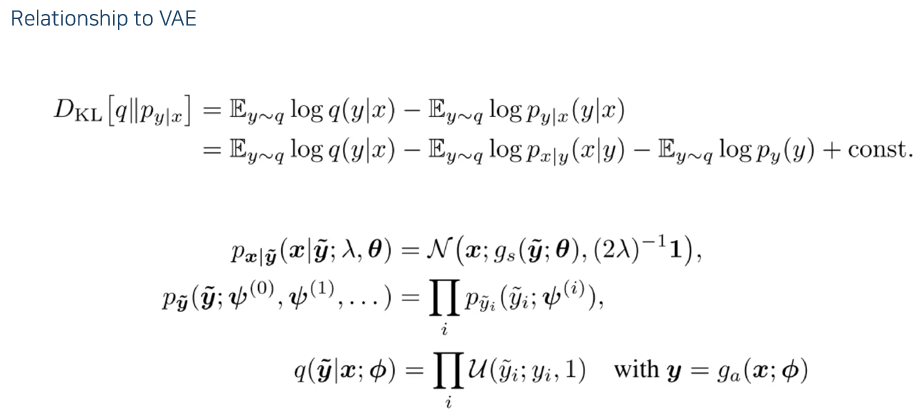
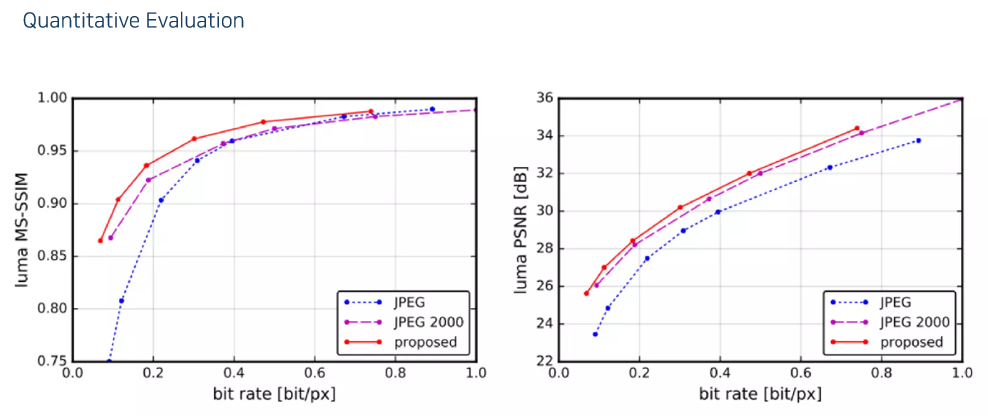
- 성능은 다음과 같고

- 오른쪽으로 갈수록 비트레이트가 작아진다. 중간 줄이 이 논문에서 제안한 방법. 위가 JPEG, 아래가 JPEG 2000.