Introduction to Optimum Design

11. More on Numerical Methods for Unconstrained Optimum Design

- 이 장의 주요내용:

이동거리 계산 시 대안 방법 사용
최속강하법에 사용된 경사도 벡터 성질 설명
최적화 방법의 성능을 개선하기 위한 설계변수의 척도 사용
비제약조건 최적화에서 뉴턴법과 같은 2계법을 사용하고 그 한계 알기
비제약조건 최적화에서 준뉴턴법으로 불리는 근사 2계 방법들을 사용
제약조건 최적화 문제를 비제약조건 최적화 문제로 변환하고 이를 풀기 위해 비제약조건 최적화 방법 사용
알고리즘의 수렴성 설명
직접 탐색법의 사용과 설명

이동거리 계산을 위한 다항식 보간, 부정확 선 탐색, 경사도 벡터의 성질, 수치최적화에서 목적함수의 헤시안 행렬을 사용하는 뉴턴법, 설계변수의 척도화, 근사 2계법(준뉴턴법), 제약조건 최적화 문제를 비제약조건 최적화 방법으로 풀 수 있도록 제약조건 문제를 비제약조건 문제로 바꾸는 변환법
비제약조건 최적화 문제는 제약조건 없이 함수 \(f(x)\)를 최소화하는 \(n\)차 벡터를 찾는 것이라는 것을 상기

최적화 기법 개요
- Stiffest Descent, Conjugate Gradient
  - Stiffest Descent는 단순 1차 도함수(기울기)를 기반으로 최적화 수행
  - Conjugate Gradient는 효율적으로 수렴하지만 2차 도함수를 활용하지 않음
- Newton Method
  - 2차 도함수(헤시안 행렬)를 활용하여 빠르게 수렴
  - 하지만 계산량이 많아 비효율적일 수 있음
혼합 기법(Marquardt Method)
- 초기 단계에서는 Stiffest Descent 처럼 작동(멀리 있는 최적점을 향해 이동)
- 최적점 근처에서는 뉴턴 메서드처럼 작동(2차 함수 근사를 통해 빠르게 수렴)
- 람다(\(\lambda\)) 값을 조정하여 두 방법을 혼합적으로 사용
  - 초기에는 큰 \(\lambda\)를 사용하여 디센트 메서드처럼 작동
  - 수렴이 가까워지면 \(\lambda\)를 작게 줄여 뉴턴 메서드로 전환
준뉴턴 방법(Quasi-Newton Method)
- 뉴턴 메서드의 헤시안 계산 부담을 줄이기 위해 헤시안이나 그 역행렬을 근사
  - 대표적인 방법 - DFP(Davidon-Fletcher-Powell), BFGS(Broyden-Fletcher-Goldfarb-Shanno)
- 인공지능 최적화에서 L-BFGS가 자주 사용됨
- 2차 도함수를 직접 계산하지 않아 효율적이지만 근사에 따른 오차 발생 가능
0차 기법(Zero-order Methods)
- 기울기(1차 정보)나 헤시안(2차 정보)을 사용할 수 없는 경우 적용
  - 예 - 함수가 미분 불가능하거나 기울기 계산이 비싸거나 불가능한 경우
- 대표적 기법
  - Univariate Search - 각 변수에 대해 반복적으로 최적화 수행 (비효율적이고 수렴 속도가 느림)
  - Hooke-Jeeves 방법 - 탐색 방향이 고정되지 않으며, 탐색 단계와 패턴 탐색 단계를 활용해 효율 개선
주요 포인트 요약
- Marquardt Method - 하이브리드 기법으로 초기에는 디센트 방식, 최적점 근처에서는 뉴턴 방식 사용
- 준 뉴턴 기법 - 헤시안을 직접 계산하지 않고 근사로 처리하여 계산 효율성 증가
- 0차 기법 - 기울기 정보를 사용할 수 없는 경우 대안으로 사용되며, 인공지능과 비선형 최적화에서 일부 활용됨.
관련 이론 및 확장
- 다양한 직접 탐색법(Direct Search Methods)과 심플렉스(Simplex) 방법 소개
- 각각의 방법은 문제의 성격(예 - 미분 가능성, 계산 복잡도)에 따라 선택적으로 사용.

결론 - 최적화 기법은 문제 상황에 따라 1차, 2차 또는 0차 정보를 활용하며, 적절한 기법을 조합해 효율성과 정확성을 동시에 추구해야 함.

11.1 Polynomial interpolation method

Instead of using golden section method, polynomial interpolation method can be used
Polynomial Approximation

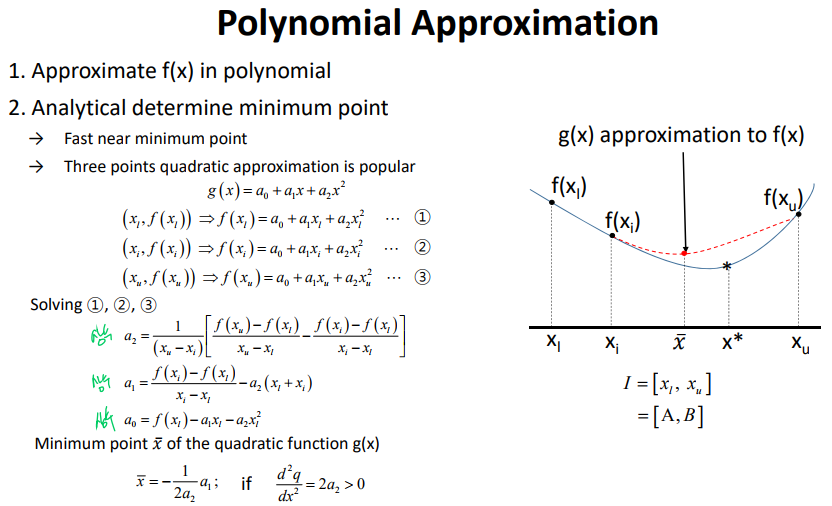
“Robust quadratic fit sectioning algorithm” by Brent(1973)

→ Idea: use quadratic polynomial approximation whenever possible, otherwise, use golden section method.

처음에 Poly 써서 값 하나 찾아놓고 이후 골든섹션 쓰는 느낌. poly 쓸 수 있으면 무조건 poly 쓰기!!

11.4 Newton method

Second-order derivative (i.e. Hessian) is used.

cf) Steepest descent method: \(\tilde{d}^k = -\tilde{\nabla}f(\tilde{x}^k)=-\tilde{g}^k\)

\(\quad\) Conjugate gradient method: \(\tilde{d}^k = -\tilde{g}^k + \beta^{k-1}\tilde{d}^{k-1}\)

\(\quad \rightarrow\) 이 방법들은 First-order derivative information을 사용
For any quadratic function with P-D Hessian

the Newton method converges just one iteration

\(f(\tilde{x}^{k+1}) = f(\tilde{x}^k + \alpha \tilde{d}^k) = f(\tilde{x}^k + \Delta\tilde{x})\)

\(= f(\tilde{x}^k) + \tilde{\nabla}f(\tilde{x}^k)\Delta\tilde{x}+\frac{1}{2}\Delta\tilde{x}^T\tilde{\nabla}^2f(\tilde{x}^k)\Delta\tilde{x}\)

This function is quadratic in terms of \(\tilde{\partial}x\) (?)

To minimize \(f, \quad \frac{\partial f}{\partial \Delta \tilde{x}} = 0\)
Remark
1. \(\frac{n(n+1)}{2}\) Second-order derivatives of \(f(x)\) is required to compute the Hessian,
  
  \(n\): number of design variables.
  
  \(n^2\)이 아닌 \(\frac{n(n+1)}{2}\)만 제공하면 됨
2. cannot be used if \(\tilde{\nabla}^2f=0\) or \(\tilde{\nabla}^2f\): Not P-D
  
  분모가 0이 되면 안되므로 / 아래로 볼록해야 함

11.4? Marquardt Method (혼합 기법)

…

Modified (Quasi) Newton Method
- The classical Newton method is not guaranteed to converge into a local minimum point, even with the use of second-order derivative information, which requires large calculation. This can be corrected if 1D line search is incorporated.

알고리즘

뉴턴법: 2계 정보 사용
준뉴턴법: 2계 정보를 1계 정보만으로 근사

방향 결정 → 2. 이동거리 결정

1D line search: golden section method, polynomial approximation

Derivative-based search: steepest descent method, conjugate gradient, modified Newton method

교재 TF 문제

Section 11.4 Search Direction Determination: Newton Method

In Newton method, it is always possible to calculate a search direction at any point. (F)* - 뉴턴 방법에서는 목적 함수의 Hessian이 필요하다. 만약 Hessian이 특이 행렬(singular matrix)이거나, 계산이 불가능한 경우(비가역적 Hessian), 탐색 방향을 계산할 수 없다. 이 상황에서는 수정된 뉴턴 방법(modified Newtorn method)을 사용해야 할 수 있다.
The Newton direction is always that of descent for the cost function. (F)* - 뉴턴 방향은 Hessian에 따라 결정된다. 만약 Hessian이 양의 정부호(P-D)가 아닌 경우, 뉴턴 방향은 하강 방향이 아닐 수 있다.
Newton method is convergent starting from any point with a step size of 1. (F) - 뉴턴 방법은 2차 수렴(quadratic convergence)을 가지지만, 초기 시작점이 목적 함수의 최소값 근처에 있지 않으면 발산할 수 있다. 또한 Hessian이 양의 정부호가 아닌 경우나 잘못된 스텝 크기를 사용하면 수렴하지 않을 수 있다.
Newton method needs only gradient information at any point. (F) - 뉴턴 방법은 gradient 뿐만 아니라 Hessian(2차 미분) 행렬 정보도 필요하다.

Section 11.5 Search Direction Determination: Quasi-Newton Methods **

The DFP method generates an approximation to the inverse of the Hessian. (T) - DFP 방법은 Hessian의 역행렬에 대한 근사값을 반복적으로 업데이트하는 방식이다. 이 방법은 초기값과 업데이트 공식을 사용하여 Hessian의 역행렬을 직접 계산하지 않고 근사값을 생성한다.
The DFP method generates a positive definite approximation to the inverse of the Hessian. (T) - DFP 방법은 근사된 역행렬이 양의 정부호(P-D)를 유지하도록 설계되었다.
The DFP method always gives a direction of descent for the cost function. (T) - DFP 방법은 P-D 역행렬 근사를 사용하여 탐색 방향을 결정하므로, 항상 하강 방향이 보장된다. 이는 목적 함수 값을 줄이는 방향으로 이동할 수 있게 한다.
The BFGS method generates a positive definite approximation to the Hessian of the cost function. (T) - BFGS 방법은 Hessian 자체에 대한 근사값을 업데이트하며, 양의 정부호를 유지하도록 설계되었다. 이는 목적 함수가 볼록(convex) 함수일 때, 수렴성을 보장한다.
The BFGS method always gives a direction of descent for the cost function. (T) - BFGS는 양의 정부호 Hessian 근사를 기반으로 탐색 방향을 결정하므로, 항상 하강 방향을 생성한다. 따라서 목적 함수 값을 줄이는 방향으로 이동이 가능
The BFGS method always converges to the Hessian of the cost function. (F) - BFGS는 Hessian에 대한 근사값을 생성하지만, 수렴 과정에서 생성된 근사값이 실제 Hessian에 도달하지 않을 수 있다. 특히, Hessian이 시간에 따라 변하거나 비선형성이 강한 경우에는 실제 Hessian과 차이가 발생할 수 있다.