On this page
Introduction to Optimum Design
10. Numerical Methods for Unconstrained Optimum Design
- 이 장의 주요내용:
평탄 최적화 문제의 반복적인 수치 탐색법 개념 설명
최적설계를 위한 경사도 기반 탐색법에서 두 가지 기본 계산: (1) 탐색방향의 계산, (2) 탐색방향에서 이동거리 계산
비제약조건 최적화에서 강하방향의 기본적 개념 설명
비제약조건 최적화에서 주어진 탐색방향에 대하여 강하방향 확인하기
최속강하법과 공액경사법에서 탐색방향 계산하기
구간감소법을 이용한 탐색방향에서 이동거리 계산하기
최적해 접근 방법
해석적 솔루션: 수학적 해석을 통해 에러 없이 해를 찾는 방법
수치적 방법(Numerical Method): 근사해를 찾으며 항상 에러가 존재할 수 밖에 없다. 특정 오차 임계값 이하일 경우 해로 간주
비제약조건 최적설계 문제
1차원 문제: 하나의 설계 변수를 가지는 문제
다차원 문제: 여러 설계 변수를 가지는 문제 (1차원 문제로 환원 가능)
초기 점 설정과 업데이트: 초기 점에서 출발하여 비용 함수가 최소화되는 방향으로 이동하며, 각 단계마다 새로운 점을 시작점으로 삼아 반복
1차원 탐색 - 선 탐색, 1D 탐색
경사도 기반 최적화 방법
경사 하강법(Steepest Descent Method)
기울기 방향 탐색: 최소화 할 함수의 기울기를 계산하여 가장 급격히 감소하는 방향으로 이동
단계적 이동: 특정 거리만큼 이동 후 기울기를 다시 계산하여 방향을 정하고, 이 과정을 반복해 최적해에 도달
\(\tilde{x}^{k+1} = \tilde{x}^k + \Delta \tilde{x}^k;\quad k=0,1,2,...\)
\(\Delta \tilde{x}^k = \alpha_k d^k\), \(\alpha\)는 이동거리 (>0), \(d\)는 ‘바람직한’ 탐색 방향
목적함수의 gradient와 바람직한 방향 \(d\)(강하방향)의 내적은 <0 이어야 함
\(c \cdot d < 0\) → 강하조건
- 이동거리 계산을 위한 해석적 방법
\(f(\alpha)\)가 간단한 함수라면 \(\alpha_k\)를 결정하기 위해 4.3절의 필요조건, 충분조건 사용 가능
필요조건: \(\frac{df(\alpha_k)}{d\alpha}=0\)
충분조건: \(\frac{d^2f(\alpha_k)}{d\alpha^2}>0\)
\(\Delta f(\tilde{x}^{k+1}) \cdot \tilde{d}^k = \tilde{c}^{k+1} \cdot \tilde{d}^k = 0\) → 선 탐색 종료 판정 기준
p.415 예제풀이 연습
- 이동거리 계산을 위한 수치 방법
해석적인 해를 얻는 것이 어려운 경우 알려진 방향 \(\tilde{d}^k\) 하에서 \(f(\tilde{x})\)를 최소화 할 때 \(\alpha_k\)를 찾기 위해서 수치 탐색법 사용
단봉성에 대한 가정
구간 감소법
Phase 1. 최솟값 처음 포괄하기(uniform bracketing, increasing bracketing)
- Bracketing, 초기 점을 기준으로 함수값을 비교하며 구간을 정해, 함수값이 최소화 될 가능성이 있는 구간 (A, B)를 찾는다.
Phase 2. 불확실 구간 줄이기(interval halving method, golden section method)
- 특정 구간 내에서 함수 값을 비교해, 함수 값이 더 큰 부분을 제거하여 최적해를 포함할 가능성이 높은 구간을 점차 줄여나간다.
효율성 및 비용
함수 평가 횟수: 각 단계에서 함수 평가가 필요하며, 반복 단계가 증가할수록 비용이 커진다.
비용 효율성 향상: interval halving method보다 golden section method가 더 효율적인 기법
Phase 1: uniform bracketing → increasing bracketing
Phase 2: interval halving → golden section method
Golden Section Method
The golden section method in this lecture is actually the integration of bracketing and golden section algorithm.
Phase 1 (bracketing) + Phase 2 (golden sectioning)


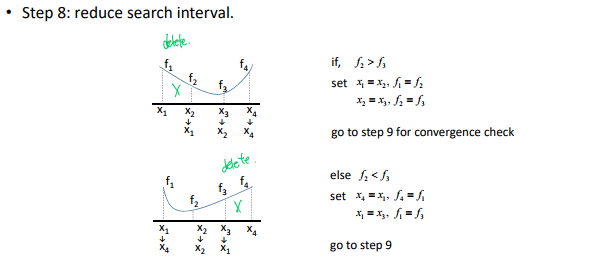

10.6 탐색방향 결정 : 최속 강하법
경사도법, 1계 방법 이라고도 함
\(\tilde{d}\)를 따라 작은 이동거리를 움직이면 목적함수가 감소해야함. 이를 만족하는 방향?: 강하방향
한 점 \(\tilde{x}\)에서 경사도 벡터는 목적함수의 최대 ‘증가’ 방향.
즉, 최대 감소 방향은 이 벡터의 반대 방향
\(\tilde{d} = -\tilde{c}, \quad (\tilde{c} \cdot \tilde{d}) = -||\tilde{c}||^2 < 0\)
헤시안의 조건수?
수렴은 보장되지만 최소점에 도달하기까지 많은 수의 반복이 요구될 수 있다.
매 반복은 서로 독립적, 이전의 반복에서 계산되었던 정보를 사용하지 않는다. 이는 비효율적일 수 있다.
1계 정보만을 사용, 수렴이 느린 이유 중 하나
최속 강하법의 수렴률은 목적함수 헤시안의 조건수에 좌우됨. 조건수가 크다면 이 방법의 수렴률이 느리다.
목적함수의 대부분 감소는 초반 몇 번의 반복으로 이루어지고 그 다음 반복부터는 이런 감소가 눈에 띄게 느려짐.
Typical search method
Look for the direction of the steepest descent.
Find \(\alpha\) to minimize \(f(\tilde{x_0} + \alpha \tilde{d}_0)\) → 1D min. problem
Update the search point \(\tilde{x}_{new} = \tilde{x}_{old} + \alpha \tilde{d}_0\)
Repeat (1) to (3) until convergence.
Consider the update rule \(\tilde{x}^{k+1} = \tilde{x}^k + \alpha \tilde{d}^k\) (여기서 \(\tilde{d}^k = -\tilde{\nabla} f,\quad \alpha>0\))
To reduce the function value, \(f(\tilde{x}^{k+1}) < f(\tilde{x}^k)\)
\(f(\tilde{x}^{k+1}) = f(\tilde{x}^k + \alpha \tilde{d}^k)\)
\(\quad\quad\quad\quad = f(\tilde{x}^k) + \alpha \tilde{\nabla} f^T(\tilde{x}^k) \cdot \tilde{d}^k\quad\) (ignore high order term \(+O(\alpha^2)\)) 테일러 급수 확장
To satisfy \(f(\tilde{x}^{k+1}) < f(\tilde{x}^k),\quad \tilde{\nabla}f^T(\tilde{x}^k)\cdot \tilde{d}^k < 0\)
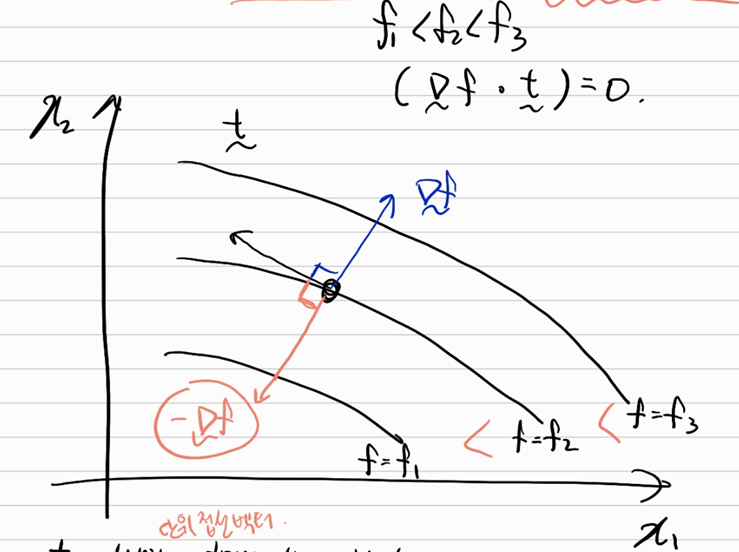
\(f_1<f_2<f_3, \quad (\tilde{\nabla}f \cdot \tilde{t})=0\)
\(\tilde{t}\): unit tangential vection 단위 접선 벡터
\(\tilde{\nabla} f\) : function increasing direction … (1)
orthogonal to the contour of \(f\) = const … (2)
from (1), (2) \(\tilde{\nabla} f\) is the direction of the fastest function increase \(\Rightarrow\) steepest ascent direction
\(\quad-\tilde{\nabla} f\): steepest descent direction \((=d^k)\)
\(\quad\tilde{d}^k = -\tilde{\nabla}f(\tilde{x}^k) =_{\text{normalize}} -\frac{\tilde{\nabla}f(\tilde{x}^k)}{||\tilde{\nabla}f(\tilde{x^k})||}\)
CONVERGENCE PROPERTY FOR THE STEEPEST DESCENT METHOD
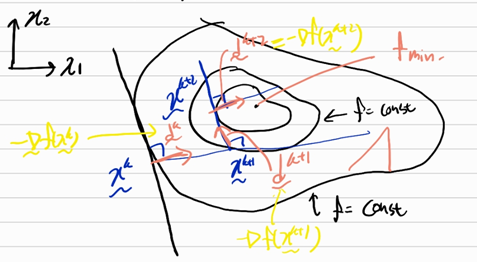
Every search direction is orthogonal to the previou search direction \(\tilde{d}^{k+1} \perp \tilde{d}^k\) (내적하면 0)
?What controls the convergence rate of the steepest descent method?e.g., \(f(x_1, x_2) = x_1^2 + ax_2^2\quad (a\ge 1)\)
원이면(a=1) 1 iteration만에 목적지에 도착, 타원이면(a>1) 혹은 찌그러져 있다면 1 보다 큰 iteration 필요
Steepest Descent Method


10.7 탐색방향 결정: 공액경사법(Conjugate gradient method)
Conjugate Gradient Method의 핵심 원리
특정 조건 하에 n회 반복(iteration)만으로 최적 해를 보장하는 방법으로 n-iteration convergence 라고 한다.
대칭이고 양의 정부호(positive definite)인 \(A\) 행렬과 목적 함수가 아래로 볼록(convex)하다는 가정이 필수적
문제 정의와 수학적 표현
목적 함수 \(Q(\tilde{x}) = \frac{1}{2}\tilde{x}^TA\tilde{x} + \tilde{B}^T \tilde{x} + C\) 형태를 가지며
(Q: quadratic function, \(A\): 대칭(symmetric) 및 양의 정부호 행렬)
최적해 \(x^*\)는 \(\tilde{\nabla} Q(\tilde{x}^*) = A\tilde{x}^* + \tilde{B} = 0\) 의 해로 정의된다.
Conjugate Directions
\(\tilde{x}^*\)는 초기값 \(\tilde{x}^0\)와 conjugate directions \(\tilde{d}^i\)의 선형 결합으로 표현될 수 있다.
\(\tilde{x}^* = \tilde{x}^0 + \sum^{n-1}_{i=1}\beta^i \tilde{d}^i\)
(\(\beta^i\): 크기를 결정하는 상수)
반복 과정
각 반복에서 다음을 수행
새로운 방향 \(\tilde{d}^i\) 계산
크기 \(\beta^i\) 추정
새로운 설계 변수 업데이트
\(\beta^i\)는 다음과 같이 계산
\[\beta^j = -\frac{d^{jT}(\tilde{B}+\tilde{A}\tilde{x}^0)}{\tilde{d}^{jT}\tilde{A}\tilde{d}^j} = - \frac{(\tilde{B}+\tilde{A}\tilde{x}^0)^Td^j}{\tilde{d}^{jT}\tilde{A}\tilde{d}^j}\]
효율성
Conjugate Gradient Method는 2차 미분값(헤시안)을 직접 계산하지 않고도 1차 미분값(그레디언트)만으로 동작하기 때문에 계산 비용이 낮다.
n차원의 설계 공간에서, 최대 \(n\)회의 반복으로 해를 찾는다.
수치적 접근 vs 이론적 접근
이론적으로는 해가 정확히 도출되지만, 수치적 방법으로는 근사치 해를 제공한다.
수치적 방법에서는 line search를 통해 반복적으로 최적 크기 \(\lambda_i\)를 결정한다.
- line search는 방향 벡터 \(\tilde{d}^i\) 와 함께 목적함수 \(Q(x)\)의 감소율을 극대화 하는 \(\lambda_i\)를 찾는 과정이다. 이 과정에서 소규모의 오차가 발생할 수 있다.
장점
2차 미분(헤시안)을 필요로 하지 않으므로 계산 효율성이 높다.
Iterative 방법이기 때문에 대규모 문제에 적합하다.
플래처와 리브스(1964)에 의해 개발된 방법을 설명
공액경사법은 매우 간단하고 효과적으로 최속강하법을 개선한 방법
최속강하 방향들은 서로 직교. 이런 성질은 최속강하법을 국소 최소점에 수렴하는 것이 보장되었다 하더라도 느리게 만드는 경향
공액경사도 방향은 서로 직교하지 않는다. 오히려 이 방향들은 서로 직교하는 최속강하 방향의 중앙을 가로지르는 경향이 있다.
그러므로 이 방향들은 최속강하법의 수렴률을 크게 향상
실제로 공액경사도 방향 \(\tilde{d}^{(i)}\)는 대칭이고 양정인 행렬 A에 대해서 직교.
\[\mathbf{d}^{(i)T}\mathbf{A}\mathbf{d}^{(j)}= 0 \quad \text{for all \ \ }i\ \text{and}\ j,\quad i \neq j\]
10.7.2 공액경사법의 수렴
- 공액경사 알고리즘은 \(n\)개의 설계변수를 갖는 양정인 이차함수에 대해서 \(n\)번의 축차 횟수로 최소를 찾는다.
10.8 Fletcher-Reeves conjugate gradient method
1121 노트
…
Remark
This method applies to non-quadratic function minimization
n iteration convergence is valid only for quadratic functions
may need to reset \(\tilde{d}^k\) for every n step.
Fletcher-Reeves Conjugate Gradient Method
The conjugate gradient method, originally due to Fletcher-Reeves, is a small modification to the steepest descent method with an enormous effect on performance.
“n iteration convergence” : a quadratic problem in \(n\) number of variables will converge in no more than n iterations

알고리즘
뉴턴법: 2계 정보 사용
준뉴턴법: 2계 정보를 1계 정보만으로 근사
- 방향 결정 → 2. 이동거리 결정
교재 TF 문제
Section 10.3 Descent Direction and Convergence of Algorithms
All optimum design algorithms require a starting point to initiate the iterative process. (T) - 최적화 알고리즘은 일반적으로 초기값을 필요로 한다.
A vector of design changes must be computed at each iteration of the iterative process. (T) - 벡터는 매 반복마다 재계산되어야 한다
The design change calculation can be divided into step size determination and direction finding subproblems. (T) - 이동 방향 설정 , 이동 거리 결정 2개로 나뉜다.
The search direction requires evaluation of the gradient of the cost function. (T)
Step size along the search direction is always negative. (F) - 스텝 크기는 음수일 필요가 없다. 이동 거리를 양수로 설정하는 것이 일반적
Step size along the search direction can be zero. (T) 특정 조건에서 0이 될 수 있다. 예를 들어 최적화가 완료된 경우, 이동할 필요가 없으므로 스텝 크기가 0이 된다.
In unconstrained optimization, the cost function can increase for an arbitrary small step along the descent direction. (F) - 임의의 작은 스텝에서도 함수 값은 항상 감소해야한다. 만약 증가한다면 이는 하강 방향이 아니게 된다.
A descent direction always exists if the current point is not a local minimum. (T) - 현재 지점이 local minimum이 아니라면, gradient가 0이 아니므로 함수 값을 감소시키는 방향(하강 방향)을 항상 찾을 수 있다.
In unconstrained optimization, a direction of descent can be found at a point where the gradient of the cost function is zero. (F) - gradient가 0이라는 것은 목적 함수가 임계점에 도달했음을 의미하고 이 경우엔 하강 방향을 정의할 수 없다.
The descent direction makes an angle of 0-90 degrees with the gradient of the cost function. (F) - 하강 방향은 gradient와 반대 방향으로 향하는 경우가 많다. 하강 방향은 보통 gradient와 90-180도 각도를 가진다. 특히, 가장 일반적인 방법인 경사 하강법에서는 하강 방향이 gradient의 음수 방향이다.
Section 10.5 Numerical Methods to Compute Step Size
Step size determination is always a 1D problem. (T)* - 스텝 크기 결정은 고정된 탐색 방향에서 이루어지므로 본질적으로 1차원 문제이다.
In unconstrained optimization, the slope of the cost function along the descent direction at zero step size is always positive. (F) - 하강 방향은 정의상 목적 함수의 기울기(gradient)를 감소시키는 방향이다. 따라서 스텝 크기 0에서의 기울기는 항상 음수이다.
The optimum step lies outside the interval of uncertainty. (F)* - 불확실성 구간은 최적 스텝이 포함되도록 정의된다. 따라서 최적 스텝은 항상 이 구간 안에 위치해야 한다.
After initial bracketing, the golden section search requires two function evaluations to reduce the interval of uncertainty. (T) - golden section search는 두 점에서의 함수 값을 평가한 후 구간을 줄이는 방식이다. 각 반복에서 구간이 축소되기 위해 두 번의 함수 평가가 필요하다.
Section 10.6 Search Direction Determination: Steepest-Descent Method
The steepest-descent method is convergent. (T) - 경사 하강법은 목적 함수가 연속적이고 미분 가능하며, 적절한 스텝 크기를 선택할 경우 수렴한다. 다만, 수렴 속도는 조건수(condition number)에 따라 느려질 수 있다.
The steepest-descent method can converge to a local maximum point starting from a point where the gradient of the function is nonzero. (F) - 경사 하강법은 하강방향으로 진행하기 때문에 local maximum이 아니라 local minimum으로 수렴한다.
Steepest-descent directions are orthogonal to each other with exact step size. (T) - 정확한 스텝 크기를 사용할 경우, 연속된 반복에서의 경사 벡터는 서로 직교한다. 이는 gradient vector의 성질과 관련
Steepest-descent direction is orthogonal to the cost surface. (F) - 하강 방향은 목적 함수(cost surface)에 수직하지 않는다. 함수의 gradient는 cost surface의 등고선(contour)에 수직하지만, 하강 방향 자체는 그 반대 방향(gradient의 음수 방향)이다.
Section 10.7 Search Determination: Conjugate Gradient Method
The conjugate gradient method usually converges faster than the steepest-descent method. (T) - 선형 독립 방향을 사용하여 각 반복에서 함수 값을 최소화하므로, 경사 하강법보다 더 적은 반복 횟수로 수렴. 특히, 이차형 함수(quadratic function)에서는 \(n\)번의 반복 내에 정확히 수렴
Conjugate directions are computed from gradients of the cost function. (T) - conjugate directions는 현재의 gradient 벡터와 이전 방향을 조합하여 계산된다.
Conjugate directions are orthogonal to each other. (F) - conjugate diretion는 gradient와는 직교하지 않는다.
The conjugate direction at the \(k\) th point is orthogonal to the gradient of the cost function at the (k+1)th point when an exact step size is calculated (T) - 정확한 스텝 크기를 계산하면, 현재 conjugate direction 방향 \(d_k\)는 다음 지점의 gradient vector \(\nabla f(x_{k+1})\)와 직교하게 된다. 이는 conjugate gradient method의 주요 성질 중 하나.
The conjugate direction at the \(k\) th point is orthogonal to the gradient of the cost function at the (k-1)th point. (F) - conjugate direction \(d_k\)는 이전 지점(\(k-1\) th)의 gradient vector와 직교하지 않는다.
- 이전 지점의 gradient 벡터와는 직교하지 않는다. 다음 지점의 gradient 벡터와는 직교한다.