Detection and Estimation (Lec 7~14 summary)

GIST 황의석 교수님 [EC7204-01] Detection and Estimation 강의 정리 내용입니다.

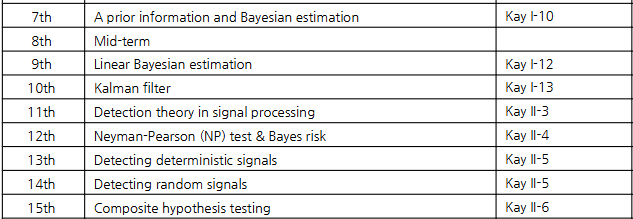
Lec 7: The Bayesian Philosophy

Bayesian 접근법은 매개변수를 확률 변수로 간주하며, 사전 분포(Prior)를 사용
최소 분산 조건이 모든 $\theta$ 값에 대해 동일하지 않기 때문에 평균적으로 최적인 추정기가 필요
MMSE 추정기: Posterior PDF의 평균, 최적추정기, 추정값 $\hat{\theta}$를 계산하는 방법

\[\hat{\theta}_{MMSE} = E[\theta|\mathbf{x}]\]

Bayesian MSE (Bmse): MMSE 추정기(혹은 다른 추정기 i.e. MAP)를 사용했을 때 달성되는 최소 MSE

\[Bmse(\hat{\theta}) = E[(\theta-\hat{\theta})^2] = E[(\theta - E[\theta|\mathbf{x}])^2]\]

사후 평균 계산:

\[p(\theta|\mathbf{x}) = \frac{p(\mathbf{x}|\theta)p(\theta)}{p(\mathbf{x})} = \frac{p(\mathbf{x}|\theta)p(\theta )}{\int p(\mathbf{x}|\theta)p(\theta)d\theta}\]

문제 풀이

MMSE 찾는 문제 (Find the Bayes estimate of $\mu$, Find MMSE estimator of $\theta$…)

최적추정기 $\hat{A} = E(A|\mathbf{x}) = \int Ap(A|\mathbf{x})dA$ 이고, 여기에서 $p(A|\mathbf{x}) = \frac{p(\mathbf{x}|A)p(A)}{p(\mathbf{x})} = \frac{p(\mathbf{x}|A)p(A)}{\int p(\mathbf{x}|A)p(A) dA}$ 이므로

이를 계산하기 위해 문제에서 주어진 $p(\mathbf{x}|A)$ 와 $p(A)$ 를 이용

Lec 8: General Bayesian Estimators

Review
- Introduced the idea of a “a priori” information on $\theta$ → use “prior” pdf: $p(\theta)$
- Define a new optimality criterion → Bayesian MSE
- Showed the Bmse is minimized by $E[\theta|\mathbf{x}]$, called “mean of posterior pdf” or “conditional mean”
Overview
- Define a more general optimality criterion
  
  → leads to several different Bayesian approaches
  
  → includes Bmse as special case
? Why?
- Provides flexibility in balancing: model, performance, and computations

…

Bayesian 추정기의 일반화:
- Quadratic cost (MMSE): Posterior의 평균 $\hat{\theta}_{MMSE} = E[\theta|\mathbf{x}]$
- Absolute cost: Posterior의 중앙값
- Hit-or-Miss cost (MAP): Posterior의 최빈값
  
  \[\hat{\theta}_{MAP} = \text{arg max}_{\theta} p(\theta|\mathbf{x})\]
  
  \[\rightarrow \hat{\theta}_{MAP} = \text{arg max}_{\theta} p(\mathbf{x}|\theta)p(\theta)\]
  
  \[\rightarrow \hat{\theta}_{MAP} = \text{arg max}_{\theta} [\text{ln} p(\mathbf{x}|\theta) + \text{ln} p(\theta)]\]
  
  arg max 이므로 비례관계만 체크하면서 전개하면 됨
  
  미분해서 0이 되는 값을 찾기
Bayesian 위험 함수 (Risk function):
Bayesian MLE

$N\rightarrow \infty,\quad \text{arg max}_{\theta} p(\theta|\mathbf{x}) \approx \text{arg max}_\theta p(\mathbf{x}|\theta)$

$\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad$ MAP $\approx$ Bayesian MLE

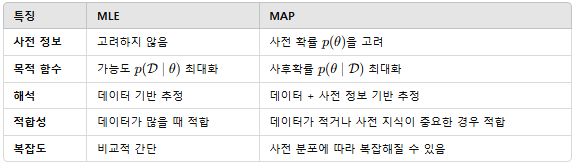
최대우도추정(Maximum Likelihood Estimation, MLE)와 최대사후확률추정(Maximum A Posteriori Estimation, MAP)의 차이

MLE: 주어진 데이터 $\mathbf{x}$에 대해 파라미터 $\theta$가 데이터를 생성할 가능도(Likelihood)를 최대화 하는 값 찾기

$\hat{\theta}_{MLE} = \text{argmax}_{\theta} p(\mathbf{x}|\theta)$ 데이터 $\mathbf{x}$ 가 주어진 파라미터 $\theta$ 하에서 관찰될 확률

직관적 이해: 데이터를 보고 “무엇이 가장 그럴듯한가?”를 판단. 완전히 데이터에 의존, 데이터가 충분하다면 정확한 추정
MAP: 사전 정보(prior)를 고려하여 데이터 $\mathbf{x}$ 가 주어진 후 파라미터 $\theta$의 사후확률(Posterior)을 최대화

$\hat{\theta}_{MAP} = \text{argmax}_\theta p(\theta | \mathbf{x})$ 베이즈 정리 및 로그를 적용하여 최적화 문제로

$\rightarrow \text{arg max}_{\theta} [\text{ln} p(\mathbf{x}|\theta) + \text{ln} p(\theta)]$

직관적 이해: 데이터를 보고 “사전 지식을 포함해서 무엇이 가장 그럴듯한가?”를 판단. 데이터가 적거나 불완전할 때 유리하며 사전 정보를 통해 추정을 보완
MAP는 MLE의 확장!

문제 풀이

MAP 찾는 문제 (Find the MAP estimator of $\theta$…)

$\hat{\theta}_{MAP} = \text{arg max}_{\theta} [\text{ln} p(\mathbf{x}|\theta) + \text{ln} p(\theta)]$

$\frac{d}{d\theta}[\text{ln} p(\mathbf{x}|\theta) + \text{ln} p(\theta)]$ 미분해서 0이 되는 값을 찾기

Lec 9: Linear Bayesian Estimation

Overview
- MMSE estimator takes a simple form when $\mathbf{x}$ and $\mathbf{\theta}$ are jointly Gaussian
  
  → It is linear and used only the $1^{\text{st}}$ and $2^{\text{nd}}$ order moments(mean and covariance).
- General MMSE estimator(without the Gaussian assumption) requires multi-dimensional integrations to implement
  
  → undesirable
- What to do if we can’t “assume Gaussian” but want MMSE?
  
  → Keep the MMSE criteria, but… restrict the form of the estimator to be LINEAR
  
  → LMMSE Estimator = “Wiener Filter”
Linear MMSE Estimation
- Scalar Parameter Case
  
  \[\hat{\theta} = \sum^{N-1}_{n=0} a_n x[n] + a_N\]
  
  Choose $a_n$’s to minimize the Bayesian MSE,
  
  \[\text{Bmse}(\hat{\theta}) = E[(\theta-\hat{\theta})^2]\]
  
  → Linear MMSE (LMMSE) estimator
  
  $\mathbf{a} = [a_0\ a_1\ ...\ a_{N-1}]^T,$
  
  $\text{Bmse}(\hat{\theta}) = C_{\theta\theta} - \mathbf{C}_{\theta x}\mathbf{C}^{-1}_{xx}\mathbf{C}_{x\theta}$
  
  $\quad\quad\quad\quad\quad$ (prior - reduce)
- $\hat{Y} = aX + b$ 로 표현?
  
  \[a = \frac{\text{Cov}(X,Y)}{\sigma_X^2}, \quad b=\mu_Y - a\mu_X\]
  
  $\text{Cov}(X,Y) = E[XY]-E[X]E[Y]$
GEOMETRICAL INTERPRETATIONS

…

Sequential LMMSE Estimation
- Data model:
\[ x[n-1] = \mathbf{H}[n-1]\boldsymbol{\theta} + \mathbf{w}[n-1] \]

\[\rightarrow \mathbf{x}[n] =\begin{bmatrix}\mathbf{x}[n-1] \\ x[n]\end{bmatrix}=\begin{bmatrix}\mathbf{H}[n-1] \\ \mathbf{h}^T[n]\end{bmatrix}\boldsymbol{\theta} +\begin{bmatrix}\mathbf{w}[n-1] \\w[n]\end{bmatrix}=\mathbf{H}[n]\boldsymbol{\theta} + \mathbf{w}[n]\]

$\mathbf{x}[n-1]$ 까지의 데이터를 기반으로 구한 추정치 $\hat{\boldsymbol{\theta}}[n-1]$ 이 있을 때 새로운 데이터 $x[n]$ 이 들어오면 이를 기반으로 추정치 $\hat{\boldsymbol{\theta}}[n]$ 을 갱신하는 것
S-LMMSE Estimation: Vector space approach
- $\tilde{x} = x[1] - \hat{x}[1|0]$ : new information from new sample : innovation
…

…

…
Wiener Filtering
- 평균이 0이고 정상성($E[X(t)] = \mu,\quad \text{Cov}(X(t_1), X(t_2)) = E[(X(t_1)-\mu)(X(t_2)-\mu)] = R_{XX}(t_2-t_1),\quad t_2-t_1 = \tau$)을 가진다고 가정

Lec 10: Kalman Filters

Introduction

Wiener filter의 실용적 한계를 해결하기 위해 개발
Three keys to leading to Kalman filter
- Weiner filter: LMMSE of signal (only for stationary scalar signals and noises)
- Sequential LMMSE: sequentially estimate a fixed parameter
- State-space models: dynamical models for varying parameters
Kalman filter: 파라미터 변화는 “상태 공간” 모델을 따른다. but unknown parameter가 시간에 따라 진화할 수 있도록 허용한다.

가우시안 조건에서 최적 MMSE 추정기를 제공. 일반적으로 최적 LMMSE 추정기로 간주

…

Dynamic Signal Models
- deterministic parameter로 모델링하면 유효하지 않음 (MVUE에서 분산이 비현실적으로 커짐)
- 신호간 상관관계를 모델링하여 더 적절한 추정을 수행해야함
- 이 문제를 해결하기 위해 신호를 랜덤프로세스의 실현(realization)으로 간주하며 베이지안 접근법을 사용
- 신호평균이 알려져 있다고 가정, 평균을 제거하고 나중에 추가
- A simple model to specify the correlation: first-order Gauss-Markov process (직전 상태에만 영향을 받음, $p(s[n]|s[n-1], s[n-2],...) = p(s[n]|s[n-1])\ $)
- Dynamical or state model: 현재 출력은 이전 상태와 현재 입력에만 의존
…
Scalar Kalman Filter
- Prediction: $\hat{s}[n|n-1] = a\hat{s}[n-1|n-1]$
- Minimum Prediction MSE: $M[n|n-1] = a^2 M[n-1|n-1] + \sigma^2_u$
- Kalman Gain: $K[n] = \frac{M[n|n-1]}{M[n|n-1]+\sigma_n^2}$
- Correction: $\hat{s}[n|n] = \hat{s}[n|n-1] + K[n](x[n]-\hat{s}[n|n-1])$ (predict + Kalman Gain(innovation - predict))
- Minimum MSE: $M[n|n] = (1-K[n])M[n|n-1]
SCALAR KALMAN FILTER - PROPERTIES
1. Kalman filter는 sequential MMSE estimator(LMMSE for non-Gaussian)의 확장. $a=1, \sigma_u^2=0$ 일 경우 칼만 필터의 특수한 형태
2. No matrix inversions are required
3. The kalman filter is a time varying filter.: first order recursive filter with time varying coefficients
4. 칼만 필터는 스스로의 성능을 측정
5. 예측단계: 오차 증가, 갱신단계: 오차 감소
6. 기본적으로 1단계 예측을 수행. $Q_k\rightarrow \infty$로 가정하면 다중단계 예측도 가능
7. 칼만 필터는 미세조정 시퀀스를 기반으로 동작, 화이트닝 필터로 간주될 수 있다.
8. 가우시안 신호가 아니어도 최적의 LMMSE 추정기로 작동
VECTOR KALMAN FILTER
Wiener Filter 와 Kalman Filter의 비교
- Domain: Wiener는 Stationary signals, Kalman은 Dynamic systems
- Noise Assumptions: Wiener는 Stationary, PSD known. Kalman은 White Gaussian, known covariances
- Model: Wiener는 PSD-based, Kalman은 State-space equations

여기부터 Detection

Lec 11: Statistical Decision Theory 1

Overview
- Theory of hypothesis testing
- Simple hypothesis testing problem with completely known PDF
- Complicated hypothesis testing problem with unknown PDF
- Primary approaches
  - Classical approach based on the Neyman-Pearson theorem
  - Bayesian approach based on minimization of the Bayes risk

…

Type 1 Error: $H_0$가 참인데 $H_0$을 기각 (False Alarm)
Type 2 Error: $H_0$을 기각해야 하는데 기각하지 못함 (Miss)
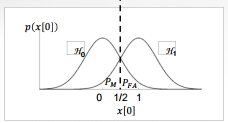
두개의 Error를 동시에 줄이는 것은 불가능
Threshold 를 잡은 시점에서 좌는 $H_0$, 우는 $H_1$
Neyman-Pearson 기준: 고정된 제 1종 오류 확률 $P_{FA}$ 에서 검출확률 $P_D$를 최대화
Type 1/2 오류 확률:

\[P_{FA} = P(H_1;H_0), \quad P_D = P(H_1;H_1) = 1- P(H_0;H_1) = 1-P_M\]

우도비 검정 LRT을 기반으로 임계값 이상일 때 $H_1$을 선택

\[L(x) = \frac{p(\mathbf{x};H_1)}{p(\mathbf{x};H_0)} > \gamma\]
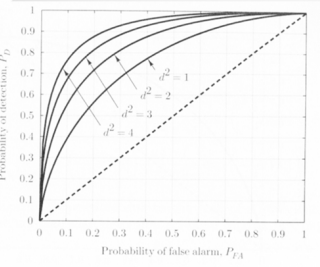
Receiver Operating Characteristics(ROC)

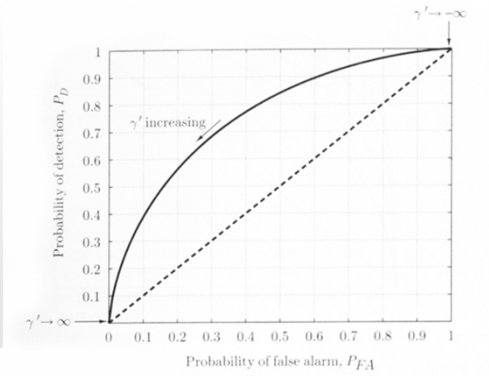
$P_{FA}$와 $P_D$ 간의 관계를 나타냄. 왼쪽 위로 갈수록 좋다.
BAYES RISK
MULTIPLE HYPOTHESIS TESTING

문제풀이

N 구하는 공식 $\frac{(Q^{-1}(P_{FA})-Q^{-1}(P_D))^2}{SNR}$

$SNR = \frac{A^2}{\sigma^2}$

Lec 12: Deterministic Signal Detection

Overview
- Detection of a known signal in Gaussian noise
  - NP criterion or Bayes risk criterion
  - The test statistic is linear funtion of the data due to the Gaussian noise assumption
  - The detector resulted from these assumptions is called the matched filter

…

Gaussian 노이즈에서의 알려진 신호 검출
가우시안 노이즈를 가정한 경우, 매치드 필터가 사용됨
매치드 필터:
- Neyman-Pearson(NP) criterion 사용
- 입력신호와 충돌하지 않도록 주파수 대역에서 신호를 강조하며 최적 SNR 달성
- 잡음이 없는 경우, 매치드 필터 출력은 단순히 신호 에너지가 됨
- Correlator
\[T(\mathbf{x}) = \sum^{N-1}_{n=0}x[n]s[n]\]
Generalized Matched Filters
- 상관 잡음을 고려한 매치드 필터의 확장
- 잡음이 non-stationary 일 경우 잡음 공분산 행렬 활용
\[T(\mathbf{x}) = \mathbf{x}^{T}\mathbf{C}^{-1}\mathbf{s} > \gamma'\]

If we let $\mathbf{s'} = \mathbf{C}^{-1}\mathbf{s},\quad T(\mathbf{x}) = \mathbf{x}^T\mathbf{s'}$ : correlation with modified signal
- Prewhitening …
MULTIPLE SIGNALS

Lec 13: Random Signal Detection

Overview
- Detecting random Gaussian signals
  - Some processes are better represented as random(e.g. speech)
    
    → Rather than assume completely random, assume signal comes from a random process of known covariance structure

…

랜덤 Gaussian 신호의 검출 (신호가 완전히 랜덤이라기 보다는 공분산 구조가 알려진 랜덤 프로세스로 가정)
추정기-상관기 (Estimator-Correlator):
- Generalization of energy detector to signals with arbitarary covariance matrix:
  
  \[ \mathbf{x} \sim \begin{cases} N(\mathbf{0}, \sigma^2 \mathbf{I}) & \text{under } H_0 \\ N(\mathbf{0}, \mathbf{C}_s + \sigma^2 \mathbf{I}) & \text{under } H_1 \end{cases} \]
- NP detector:
  
  Decide $H_1$ if
  
  \[T(\mathbf{x}) = \mathbf{x}^T\hat{\mathbf{s}}>\gamma'', \quad T(\mathbf{x})=\sum^{N-1}_{n=0}x[n]\hat{s}[n]\]
  
  $\hat{s} = \mathbf{C}_S(\mathbf{C}_s+\sigma^2\mathbf{I})^{-1}\mathbf{x}$
  
  $T>\eta$ 일 때 $H_1$ 선택
LINEAR MODEL
GENERAL GAUSSIAN DETECTION

Lec 14: Statistical Decision Theory 2

Review & Overview
- Neyman-Pearson criteria (max $P_D$ s.t. $P_{FA}$=constant) : Likelihood ratio test, threshold set by $P_{FA}$
- Minimize Bayesian risk(assign costs to decisions, have priors of the different hypotheses) : Likelihood ratio test, threshold set by priors + costs
  - minimum probability of error = Maximum A Posteriori detection
  - maximum likelihood detection = minimum probability of error with equal priors
- Known deterministic signals in Gaussian noise: Correlators
- Random signals: estimator-correlators, energy detectors
All assume knowledge of $p(x;H_0)$ and $p(x;H_1)$

? What if don’t know the distribution of $x$ under the two hypotheses?

? what if under hypothesis 0, distribution is in some set, and under hypothesis 1, this distribution lies in another set - can we distinguish between these two?

→ Composite Hypothesis Testing
복합 가설 검정(Composite Hypothesis Testing):
- Generalized Likelihood Ratio Test(GLRT):
  
  \[\Lambda(\mathbf{x}) = \frac{\text{max}_{\theta\in\Theta_1}f(\mathbf{x}|\theta, H_1)}{\text{max}_{\theta\in\Theta_0}f(\mathbf{x}|\theta, H_0)}\]
UMP 검정: 가능한 모든 매개변수 값에 대해 성능이 최적화된 검정

Homework

hw6

★P1: Find the Bayes estimation of $\mu$.
- Posterior의 Expection 구하기. $E[\mu|\tilde{X}]$
★P2: Find the MAP estimator of $\theta$ / Find MMSE estimator of $\theta$
- Posterior의 최빈값 구하기. 지수함수가 단조함수임을 이용해 그림으로. 다른 경우엔.. 11.4 풀이 확인
- Posterior의 Expection 구하기. $E[\theta|y]$
★P3: Find the MMSE Estimator of $\theta$
- conditional independence를 이용하는 문제
(10.4): uniform prior PDF $\cal{U}[0,\beta]$가 주어 졌을 때 MMSE estimator of $\theta$를 찾고 $\beta$가 매우 커졌을 때 어떤 일이 벌어지는 지
- $\beta$가 매우 커지면, 즉 사전 정보가 거의 없으면 사후확률분포는 likelihood에 의해 지배되며 $\theta$의 MMSE 추정기는 데이터의 최대 관측값 $x_{max}$에 크게 의존하게 된다.
(10.12): Joint Gaussian 문제. 최대값, 평균, …
- 정규분포에서 조건부 평균은 최우 추정치와 일치한다.
(11.3): posterior PDF가 주어지고 (지수함수) find the MMSE and MAP
- MAP는 지수함수가 단조함수임을 이용해 그림으로 해결하고 MMSE는 치환적분
(11.4): Find the MAP estimator of A
- $x[n] = A + w[n]$ 신호에 대해 MAP를 찾는 문제,
  
  $\text{ln}p(A|\tilde{X}) = \text{ln} p(\tilde{X}|A) + \text{ln} p(A)$ 에서 이를 최대화 하는 $A$값을 찾기 위해 $A$에 대해 미분해서 0이 되는 값을 찾음
(11.16): $x[n] = A + Bn + w[n]$ 신호에 대해 MMSE estimator를 찾고 Bmse를 계산한 뒤 사전 정보가 A와 B중 어떤 파라미터에 더 큰 benefit을 주는 지.
- prior 분산이 작은 파라미터가 사전 정보로부터 더 많은 이득을 얻는다.

hw7

★P1: $Y=X^2$ 의 $X$에 대한 LMMSE 값을 구하라, 해당 추정값의 MSE를 구하라
★P2: Kalman gain $K[n]$ 추정 오차 분산 $M[n]$을 구하라. / 사전 정보가 없을 경우, 추정 값이 단순히 sample mean이 되는 것을 증명
★P3: 스칼라 상태 - 스칼라 관측 칼만 필터 모델, innovation sequence를 구하고, 이것이 백색 잡음(white noise)인지 여부 판별
(12.1): Quadratic estimator의 coefficient를 구하고 LMMSE 추정기를 구하고 두 추정기의 MSE를 비교
(12.11): $C^{-1}_{xx}$와 $A$의 관계, Gram-Schmidt, whitening, …
(13.4): 공분산 관계, 공분산 전파 방정식
(13.15): 최적의 l 스텝 예측기, 가우스 마르코브 프로세스, …

hw8

★P1(3.4): DC level in WGN detection 문제에서 $P_{FA}, P_D, SNR$이 주어졌을 때 number of samples $N$ 구하기
- $N = \frac{(Q^{-1}(P_{FA})-Q^{-1}(P_D))^2}{SNR}, \quad SNR = \frac{A^2}{\sigma^2}$
  
  Q 함수표 이용해야 함
★P2(4.10): 공분산 행렬이 주어졌을 때 Find the matrix prewhitener $D$
- 고유값, 고유벡터 계산 및 주어진 식 이용하기 $C^{-1} = D^TD$ 등
(3.6): Determine the NP detector and its detection performance to show that it is the same as for A>0
- $T(\mathbf{x})$ 구하고 NP 검출기 계산 후 $P_{FA}$, $P_D$ 계산 및 A<0 과 A>0의 성능 비교
(3.12): 두 유니폼 pdf를 가진 가설로부터 Design a perfect detector for problem
- 두 가설의 pdf가 서로 겹치지 않게 설정하여 완벽한 검출기 만들기.
(3.18): Find the MAP decision rule / 각 케이스의 decision regions 를 보이고 설명하기
- MAP 결정 규칙 계산을 위해 우도 함수 계산, 결정 영역 설정…
(4.6): $s[n] = Ar^n$ in WGN with variance $\sigma^2$ 신호에 대해 Find NP detector and its detection performance.
- NP 검출기의 가설 설정 및 우도비 검정, 결정규칙을 정하고 … … $N\rightarrow\infty$ 에서의 성능
(4.19): $R^2$ 평면에서 최소 오류 확률을 달성하는 결정 영역 그리기, 이 때 사전확률 $P(H_0)$과 $P(H_1)$이 같지 않을 수 있음
(4.24): 오류 확률 $P_e$를 최소화하는 최적 수신기(최적 결정 규칙) 구하기 …

hw9 (Lec 13)

★P1(5.14): Show the NP detector for a Gaussian rank one signal …
- Gaussian random process → 신호가 랜덤, Estimator-correlator의 $\hat{s}$ = $\mathbf{C}_s(\mathbf{C}_s + \sigma^2 \mathbf{I})^{-1}\mathbf{x}$ 사용!
  
  $T(\mathbf{x}) = \mathbf{x}^T\mathbf{s}$ … 검정통계량이 $h^Tx$가 아닌 $(h^Tx)^2$ 이므로 카이제곱을 써야한다…
★P2(6.2): 두 개의 샘플이 지수분포로 주어져 있을 때 UMP test가 존재하는지 확인하고 $T(\mathbf{x})$와 $P_{FA}$를 찾아라
- 지수분포 합의 분포
(5.16): Rayleigh fading 환경에서의 수신된 신호를 기반으로 한 ML 추정기 구하기
(5.17): Deflection coefficient, 위상 오차의 영향…
(6.8): GLRT
(6.15): GLRT, Rao Test, Wald test