On this page
TS2Vec: Towards universal representation of time series(AAAI 2022)
1. Introduction
시계열 데이터는 금융 시장, 수요 예측, 기후 모델링 등 다양한 산업 분야에서 중요한 역할
이러한 시계열 데이터에 대해 범용적인(universal) 표현을 학습하는 것은 기초적이면서도 도전적인 과제
많은 기존 연구들(Tonekaboni et al., 2021; Franceschi et al., 2019; Wu et al., 2018)은 인스턴스 수준(instance-level)의 표현 학습에 집중
- But 인스턴스 수준의 표현은 시계열 예측(forecasting)이나 이상 탐지(anomaly detection)과 같은 미세한 수준(fine-grained)의 표현을 필요로 하는 작업에는 적합하지 않다. 이러한 작업에서는 특정 시점이나 특정 구간에 대한 정밀한 정보를 필요로 하며, 전체 시계열을 하나로 압축하 포현은 만족스러운 성능을 제공하기 어렵다.
기존 방법들 중 다중 스케일(multi-scale)의 문맥 정보를 구분하여 학습하는 경우는 드물다. 직관적으로 다중 스케일의 특징은 다양한 의미 수준을 제공하며, 표현의 일반화 능력을 향상시킬 수 있다.
transformation-invariance, cropping-invariance와 같은 강한 귀납적 편향(inductive bias)는 컴퓨터 비전(CV)나 자연어 처리(NLP)에서의 경험을 그대로 적용한 것이나 시계열 데이터에는 항상 적절하지는 않다.
⇒ TS2Vec이라는 새로운 범용 대조 학습 프레임워크를 제안
2. Method
2.1 Problem Definition
N개의 instance를 가진 time series \(\cal{X}=\{x_1, x_2, ..., x_\text{N}\}\)가 주어졌을 때,
각각의 \(x_i\)를 가장 잘 표현하는 representation \(r_i = \{r_{i,1}, r_{i,2}, ..., r_{i,T}\}\) 를 매핑하는
nonlinear embedding function \(f_\theta\)를 얻는 것
\(x_i \in \mathbb{R}^{T\times F}\)
\(r_{i,t} \in \mathbb{R}^{K}\) for each timestamp \(t\), where \(K\) is the dimension of representation vectors
\(r_i \in \mathbb{R}^{T\times K}\)
\(r=f_\theta(x)\in\mathbb{R}^{T\times K}\) 이며 timestamp level representation이다.
필요시 Max pooling을 적용하여 instance level representation으로 만든다.
? Instance level representation ↔︎ timestamp level representation
인스턴스 수준 표현 : 하나의 시계열 인스턴스(전체 시퀀스) 전체를 하나의 고정길이 벡터로 요약한 표현.
즉, 주어진 시계열 \(x=[x_1, x_2, ..., x_T]\in \mathbb{R}^{T\times F}\)에 대해 임베딩 함수 \(f_{\theta}\)가 전체 시계열을 하나의 벡터 \(r\in \mathbb{R}^K\)로 매핑하는 방식.
\(r=f_{\theta}(x)\)

Instance-level representation은 “전체 시계열을 대표하는 하나의 벡터 표현”
2.2 Model Architecture
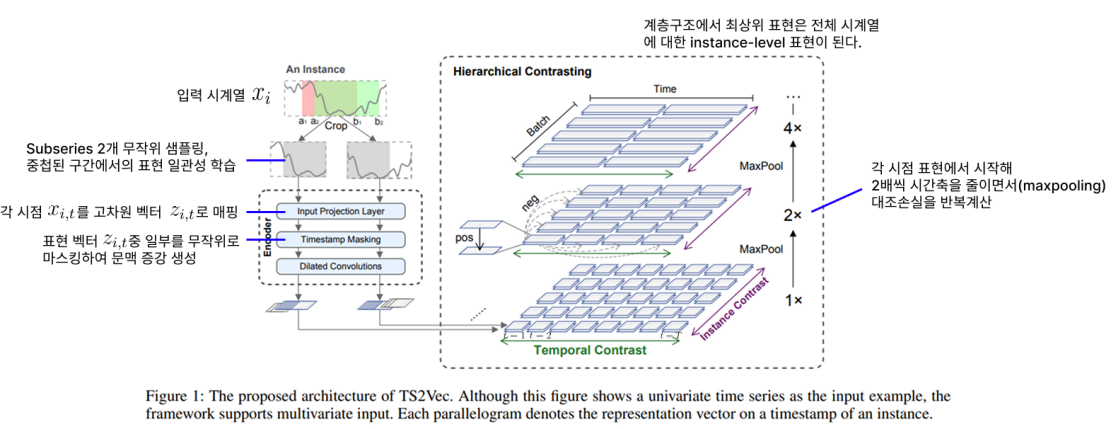
1. Input Projection Layer
각 시점의 원본 입력 \(x_t \in \mathbb{R}^F\) 를 고정된 차원의 임베딩 \(z_t \in \mathbb{R}^d\) 로 매핑
목적: 다양한 feature 차원의 입력을 고정된 차원으로 투영하여 CNN에서 처리 가능하게 만듦.
방식: 1D convolution 또는 linear projection 사용 가능
2. Timestamp Masking
입력 시계열의 일부 시점을 마스킹 (zero-out) 하여 문맥(view) 변화를 만들어냄 (augmentation 효과)
목적:
contextual consistency 기반 positive pair 생성을 위해 필요
self-attention처럼 특정 시점의 정보 없이 주변 문맥으로 표현을 학습하도록 유도
이 과정을 통해 robust한 표현 학습 가능
방식: 각 시점 \(t\) 에 대해 마스킹 확률 \(p=0.5\) , 마스킹된 입력은 여전히 모델로 forward되며, 해당 시점의 표현은 문맥에 의존하여 생성
3. Dilated CNN 인코더
핵심 인코더 구조는 dilated convolutional network (확장 합성곱 CNN)
10개의 residual 블록으로 구성됨.
각 블록은 다음을 포함: 1D dilated convolution, ReLU, layer normalization, residual connection
? Dilated convolution
커널 사이에 “공백”을 두어 receptive field를 넓힘
시간 정보를 더 멀리서도 통합할 수 있음
시계열의 다양한 길이 패턴에 반응 가능 (다중 스케일 학습 효과)
결과적으로, 이 구조는 각 시점의 표현 \(r_t\) 이 넓은 시간 문맥을 반영하도록 해줌.
Input Projection - feature 정규화, 다양한 입력에 대응
Timestamp Masking - context view 생성, self-supervised 학습 유도
Dilated CNN - 문맥 정보 통합, 시계열의 의존성을 반영하고 긴 범위 포착 가능
2.3 Contextual Consistency
Positive pair의 정의는 Contrastive Learning에서 핵심 요소
기존 방법:
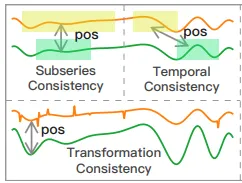
Subseries Consistency (T-Loss):
전체 시계열과 그 일부 구간 간의 표현이 가까워야 한다고 가정.
Temporal Consistency (TNC):
시간적으로 인접한 구간들은 유사한 표현을 가져야 한다고 가정.
Transformation Consistency (TS-TCC):
스케일링, 왜곡 등 다양한 변형을 가하여도 표현이 유지되어야 함을 전제.
하지만 이 저자는 위 가정에 의문을 제시한다.
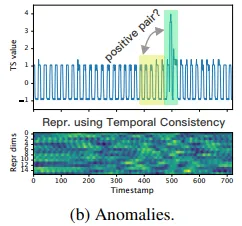
Subseries consistency는 시계열에 레벨 쉬프트(level shift)가 있는 경우 실패.
Temporal consistency는 이상치(anomalies)로 인해 잘못된 양성 쌍을 생성할 수 있음.
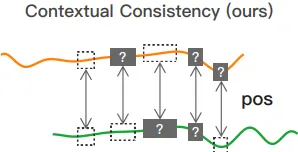
TS2Vec에서의 제안 방법: 문맥적 일관성(Contextual Consistency)
서로 다른 증강에서의 동일 시점 표현을 Positive Pair로 간주
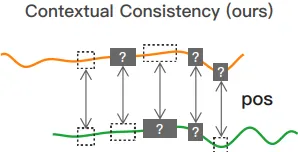
장점:
- 시계열의 크기를 왜곡하지 않으며 다양한 문맥에서도 시점 표현의 일관성을 유지하게 하여 강건한 표현을 학습
증강엔 2가지 방법을 사용
Timestamp Masking: 시점별 표현 \(z_{i,t}\)를 마스킹 (from a Bernoulli distribution with \(p=0.5\)). mask들은 인코더의 모든 forward pass 마다 독립적으로 샘플링된다.
Random Cropping: 시계열에서 2개의 subseries를 무작위로 잘라내고 중첩된 구간의 표현이 일치하도록 학습
segments는 랜덤하게, 중첩되도록 샘플링
\([a_1,b_1]\), \([a_2, b_2]\) such that \(0<a_1\le a_2\le b_1\le b_2\le T\)
(중첩된 부분: \([a_2, b_1]\))
2.4 Hierarchical Contrasting
hierarchical contrastive loss를 제안, 다양한 스케일의 표현을 학습하도록 강제한다.
Timestamp-level representation 기반으로 max pooling을 사용하여 time axis를 줄이며 대조손실을 반복 계산
Contrastive Loss
총 손실(Dual Contrastive Loss)는 다음 두 항으로 구성된다.
\(\mathcal{L}_{\text{dual}} = \frac{1}{NT} \sum_{i} \sum_{t} \left( \ell^{(i,t)}_{\text{temp}} + \ell^{(i,t)}_{\text{inst}} \right)\)
Temporal Contrastive Loss
\(\ell^{(i,t)}_{\text{temp}} = -\log \frac{\exp(r_{i,t} \cdot r'_{i,t})}{\sum_{t' \in \Omega} \left( \exp(r_{i,t} \cdot r'_{i,t'}) + \mathbb{1}_{[t \neq t']} \exp(r_{i,t} \cdot r_{i,t'}) \right)}\)
동일 시계열 \(i\), 시점 \(t\)에 대해 증강된 두 뷰 \(r_{i,t}\)와 \(r'_{i,t}\)간의 유사도 극대화, 나머지 시점들과는 구별
Instance-wise Contrastive Loss
\(\ell^{(i,t)}_{\text{inst}} = -\log \frac{\exp(r_{i,t} \cdot r'_{i,t})}{\sum_{j=1}^{B} \left( \exp(r_{i,t} \cdot r'_{j,t}) + \mathbb{1}_{[i \neq j]} \exp(r_{i,t} \cdot r_{j,t}) \right)}\)
동일 시점 \(t\)에서 다른 시계열들과의 표현은 Negative pair로 사용
두 손실은 상호보완적. 예를 들어 전력 사용량 예측에서는 instance-wise contrastive loss가 사용자 특성을, temporal contrastive loss는 시간적 추세를 학습하는 데 기여
3. Experiments
3가지 Downstream에 대한 실험 (time series classification, forecasting, and anomaly detection)
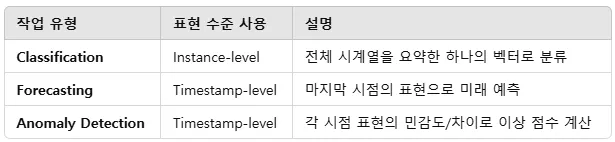
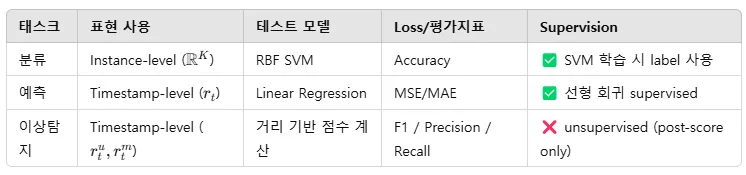
Classification:
인코더 학습 후 인코더에 입력 \(x\in\mathbb{R}^{T\times F}\)을 넣어 나온 출력 표현 \(r\in\mathbb{R}^{T\times K}\)(timestamp-level)을 Max Pooling하여 instance level representation으로 나타낸 뒤 얻은 표현 위에 RBF 커널 SVM을 훈련하여 분류. SVM은 label 사용하여 supervised 학습, 하지만 TS2Vec 자체는 미학습 상태로 고정 (frozen representation)
Forecasting:
인코더 학습 후 인코더에 입력 \(x_{t-T_l+1:t}\) (길이 \(T\))를 넣어 나온 출력 표현 \(r_t\in\mathbb{R}^K\)(마지막 시점 표현)을 이용해 Linear Regression (Ridge)모델 학습: \(\hat{x}_{t+1:t+H}=Wr_t+b\)
입력: \(r_t\)
출력: 미래 값 \(H\)개
Anomaly Detection:
인코더 학습 후 시계열을 두 번 forward pass:
Unmasked → \(r_t^u\)
Masked(마지막 시점만) → \(r_t^m\)
이후 이상 점수 계산 및 이상 여부 판정(이상 점수가 평균보다 \(\mu+\beta\sigma\) 이상이면 이상).
특징은 어떤 특정 태스크용 학습 없이도 전이(transfer)하여 anomaly scoring이 가능하다는 점
3.1 Time Series Classification
클래스 라벨이 시계열 전체(인스턴스) 에 부여되므로, instance-level representation이 필요
TS2Vec에서는 전체 시계열의 표현을 각 타임스탬프 표현에 대한 Max Pooling으로 계산.
이후 T-Loss(2019)의 평가 방식에 따라 RBF 커널을 가진 SVM을 훈련하여 분류 성능을 측정
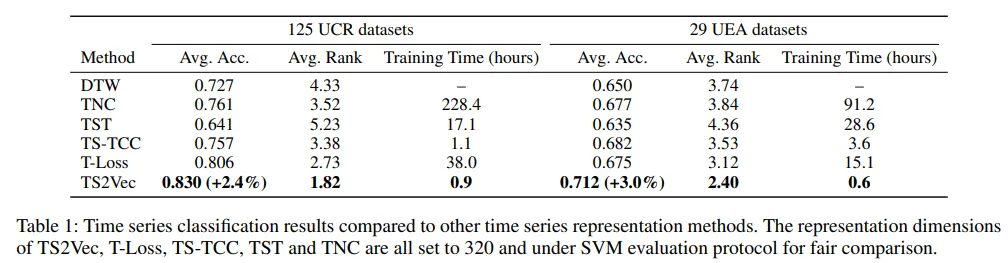
TS2Vec는 가장 빠른 학습 시간을 보이며, 효율성과 성능을 동시에 확보함.
3.2 Time Series Forecasting
시계열 예측은 과거 \(T_l\)개의 관측값 \(x_{t-T_l+1},...,x_t\) 으로 부터 미래 \(H\)개의 값을 예측하는 Task
TS2Vec에서는 마지막 시점 표현 \(r_t\)을 입력으로 받아 선형 회귀 모델을 학습하여 미래 값을 예측
예측 길이에 무관하게 표현을 한번만 학습하면 모든 \(H\)에 재사용 가능
- 하나의 표현 모델로 여러 예측 길이 (\(H)\)에 대응 가능 → 매우 범용적인 표현 학습임을 의미!
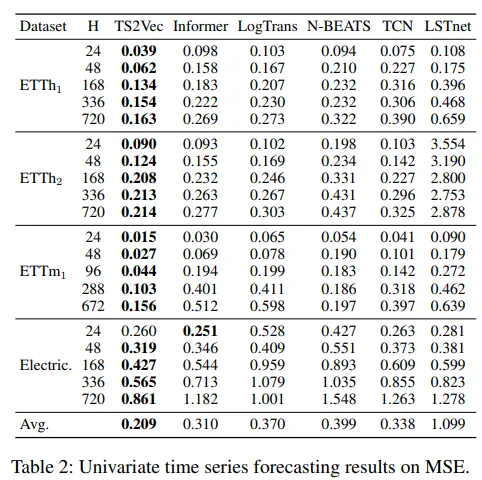
Informer 대비 주기적 패턴 예측, TCN 대비 장기 추세 포착에서 우수함을 보여줌
Informer 대비 학습 및 추론 속도 모두 우수
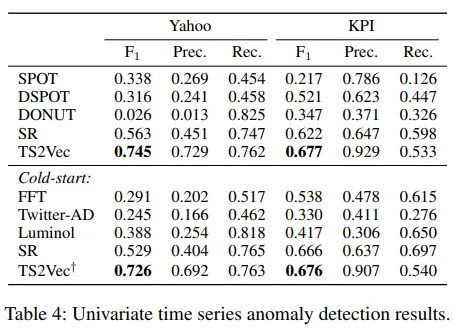
3.3 Time Series Anamaly Detection
이상 탐지는 주어진 시계열 \(x_1,x_2,...,x_t\)에서 마지막 시점 \(x_t\)이 이상치인지 여부를 판단하는 Task
여기선 streaming evaluation protocol(Ren et al. 2019)를 따른다고 한다.
TS2Vec 에서 제안한 anomaly score 계산 방법
입력 시계열을 두 번 forward pass:
- 한 번은 마지막 시점을 마스킹하여 \(r_t^m\) 계산
- 한 번은 마스킹 없이 \(r_t^u\) 계산
두 표현의 차이 L1 distance 사용:
\(α_t=∥r_t^u−r_t^m∥_1\)
과거 \(Z\)개의 평균값으로 정규화한 후, 이상 탐지 임계값을 넘으면 이상으로 판단
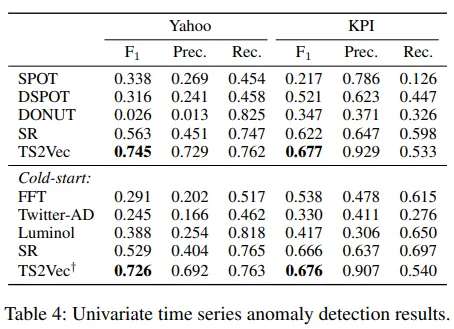
cold-start 설정에서도 TS2Vec†는 타 모델 대비 뛰어난 전이 성능을 보임.
TS2Vec은 훈련없이도 전이 가능한 표현을 학습하며 이는 범용성과 일반화 능력을 입증한다.
4. Analysis
4.1 Ablation Study (구성 요소 분석)
TS2Vec은 다양한 구성 요소의 조합으로 이루어져 있으며, 그 각각이 표현의 품질에 영향을 미친다.
이를 검증하기 위해, 구성 요소를 하나씩 제거하거나 대체한 ablation 실험 수행
No Contextual consistency
No Hierarchical contrasting - 계층적 대조 학습 제거, 단일 스케일에서만 학습
No Timestamp masking
No Random cropping
+Scale Aug
+Permute Aug
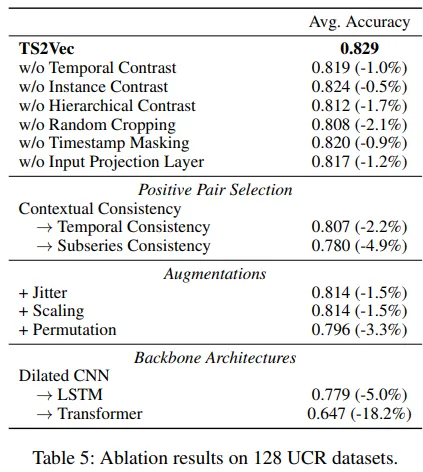
모든 구성 요소가 표현 품질 향상에 기여
특히 No Contextual Consistency와 No Hierarchy 설정에서 성능 하락이 크다.
→ TS2Vec의 핵심 기여 요소는 Contextual Consistency 기반 대조학습과 계층 구조임을 의미
+Scale Aug, Permute Aug는 오히려 성능을 떨어뜨림. → 일부 기존 방식에서 사용한 변환(augmentation)은 시계열에는 적합하지 않음
4.2 Robustness to Missing Data (결측값에 대한 강건성)
현실의 시계열 데이터는 종종 결측(missing)이 존재하므로, 표현 학습 모델의 결측값에 대한 강건성은 매우 중요
TS2Vec는 최대 50% 결측률까지도 안정적인 분류 성능 유지
T-Loss나 TS-TCC 등은 결측에 매우 취약
Dilated CNN 구조와 타임스탬프 마스킹 기반 문맥 학습이 결측 보완에 효과적
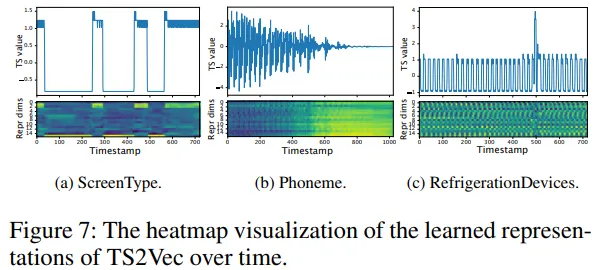
4.3 표현 시각화
Yahoo 이상 탐지 데이터셋 사용
시계열의 각 시점에 대해 표현 벡터 \(r_t\in\mathbb{R}^K\)를 추출
각 표현 벡터 간의 유사도를 시각화
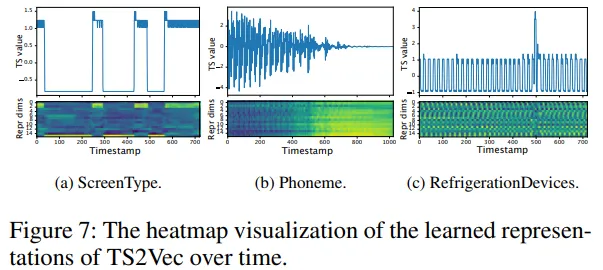
표현 간 유사도 맵(similarity heatmap)에서, 이상 이벤트 이후 시점들의 표현이 급격히 달라짐을 확인
즉, TS2Vec은 패턴의 전환점, 이상구간, 변화 지점 등을 잘 포착하고 있음을 의미
이는 이상 탐지나 구조 분석(task-agnostic) 작업에서도 표현이 유용함을 시사
5. Conclusion
TS2Vec이라는 범용 시계열 표현 학습 프레임워크 제안
TS2Vec은 시계열의 다양한 의미 수준(semantic levels)에서 표현을 학습할 수 있으며, 이러한 표현은 분류(classification), 예측(forecasting), 이상 탐지(anomaly detection) 등 다양한 downstream 작업에 유용하게 활용될 수 있다.
핵심 아이디어는 다음과 같다:
시계열의 각 시점(timestamp)에서 Contextual representation을 생성하고,
서로 다른 문맥(context)에서도 표현 간 일관성(consistency)이 유지되도록 대조학습(contrastive learning)을 수행하며,
다양한 시간 스케일에서 계층적 표현(hierarchical repressentations)을 학습함으로써,
다양한 의미 수준에서 강력하고 범용적인 표현을 획득한다.
Self Q&A
? 시계열의 3가지 downstream 태스크에 대한 테스트는 어떻게 진행하는지?
TS2Vec는 디코더 없이 인코더만 학습하고, 학습된 표현을 다양한 시계열 downstream 태스크 (분류, 예측, 이상 탐지)에 별도의 간단한 모델을 얹어서 테스트
특정 데이터셋에서 인코더를 한 번 학습한 뒤, 전이학습 없이도 표현만 고정(freeze)한 채로 간단한 모델을 얹어 3가지 태스크 모두 수행 가능
? 다른 지도학습 같은 모델과는 어떻게 비교하는지? 둘 다 데이터 기반 학습 후에 인코더, 디코더가 있는 모델은 디코더를 떼버리고 동일하게 간단한 모델을 붙여서 성능평가 하는 것?
표현 추출 이후 동일한 분류기 사용! 지도학습 모델의 표현도 디코더를 제거하거나, 중간 hidden state 또는 최종 hidden vector를 repressentation으로 추출하고 동일하게 SVM 등을 붙여 비교.
즉, 지도학습 모델이라고 해도 표현만 추출하고, 그 위에 SVM을 붙여 평가하는 방식으로 self-supervised 방식과 공정 비교함.
? 제목의 TS2Vec은 시계열을 벡터로 바꾼다는건데 차원이 TxF에서 TxK로 가잖아. 그럼 결국 아웃풋이 매트릭스 아니야?
- 여기서 Vec은 “하나의 벡터”가 아니라, 시계열 전체를 벡터 공간 상에서 표현한다는 의미적 표현. “vector 표현”을 다양한 방식으로 추출해서 downstream task에 활용하는 구조
? 여기서 나오는 instance의 의미?
“하나의 시계열 샘플”, 즉 하나의 독립적인 시계열 조각(sequence) 을 의미.
예를 들어 센서 데이터(다변량)에서 온도, 습도, 진동 3가지 센서를 100초간 수집했다고 하면
하나의 instance: \(x_i\in\mathbb{R}^{100\times 3}\)
500명의 기기에서 수집했다면: 총 \(N = 500\) 개의 instance
입력 시계열 : \(\mathbb{R}^{T\times F}\) - 원시 시계열 데이터
출력 : \(\mathbb{R}^{T\times K}\) - 시점별 임베딩 벡터 행렬
*fine-grain(세밀한 수준): 개별 시점(timestamp)이나 짧은 구간(sub-sequence) 단위의 정보 표현. [예측, 이상탐지]
*coarse-grain(거친 수준): 전체 시계열(instance 전체)을 요약한 표현. [분류, 군집화]
*streaming evaluation protocol: 시계열 이상 탐지에서 중요한 평가 방식. 시계열 데이터를 과거에서 미래로 한 시점씩 순차적으로 처리하면서, 현재 시점 \(t\) 에서 그 시점이 이상(anomaly)인지 여부를 즉시 판단하는 평가 방식. 실시간 온라인 상황을 가정한 평가방식이며 모델은 미래 데이터를 볼 수 없고, 오직 이전 시점까지의 데이터만 사용 가능하다.