On this page
Dual Cone Gradient Descent for Training Physics-Informed Neural Networks(NeurIPS 2024)

Hwang, Youngsik, and Dongyoung Lim. “Dual cone gradient descent for training physics-informed neural networks.” Advances in Neural Information Processing Systems 37 (2024): 98563-98595.
Notation
Euclidean scalar product \(⟨·,·⟩\) (내적으로 생각하면 됨)
Euclidean norm \(\|·\|\) (공간의 차원은 문맥에 따라 달라짐)
벡터공간 \(V\) 의 부분 공간 \(W\) 의 직교 여공간(orthogonal complement) \(W^⊥ := \{v\in V|⟨u, v⟩=0,\quad u\in W\}\)
벡터 \(v\in V\) 의 부분공간 \(W\) 위로의 projection \(v_{\|W}\)
별도의 언급이 없는 한, 벡터공간 \(V\)는 \(\mathbb{R}^d\) 를 의미
Contribution
Boundary condition loss와 PDE residual loss의 기울기 크기 불균형과 음의 내적(gradient conflict)이 학습 실패의 주요 원인임을 지적
이를 해결하기 위해 Multi-objective optimization의 새로운 프레임워크 Dual Cone Gradient Descent(DCGD)를 제안
이론적으로 non-convex 설정에서 DCGD 알고리즘의 수렴 특성을 분석
Helmholtz, Burgers, Klein-Gordon, 3D Helmholtz 등 여러 PDE 벤치마크와 chaotic system(Kuramoto-Sivashinsky, Double Pendulum 등)에서 기존 최적화 기법보다 더 낮은 상대 L2 오차와 더 안정적인 학습을 보임
- 특히 Adam이 실패하는 chaotic system에서도 성공적으로 수렴함을 입증
PINNs 학습 과정에서의 두 가지 문제점
PINNs의 손실 함수 \(\mathcal{L}(\theta) := \omega_r \mathcal{L}_r(\theta)+\omega_b \mathcal{L}_b (\theta)\)
Multi-objective optimization에서 표준 경사 하강법을 그대로 사용하면 잘못된 해로 수렴할 수 있다. 총 손실을 줄이는 것이 PDE 잔차 손실과 BC 손실을 모두 줄인다는 것을 보장하지 않기 때문
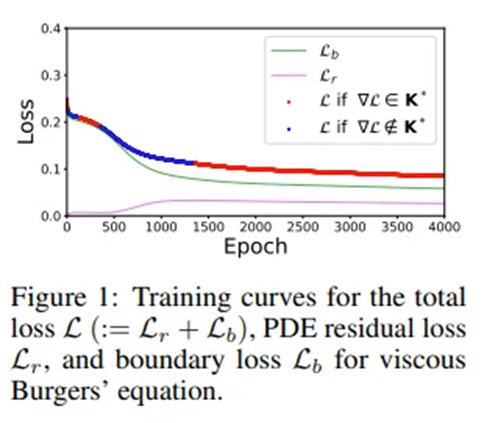
총 손실은 학습 내내 감소하지만, PDE 잔차 손실은 오히려 증가하는 역효과(adverse training)가 나타나는 모습
? 왜 PDE residual loss가 0에서 시작하는가? (맨 아래에 서술)
Conflicting gradients in PINNs
기울기 충돌(conflicting gradients): 두 기울기가 t번째 반복에서 음의 내적을 가지는 경우. \(\text{i.e.,}\ \frac{\pi}{2}<\phi_t\le \pi\)
- 영향: 충돌하는 기울기가 존재하면 한 손실 함수를 줄이기 위한 파라미터 업데이트가 다른 손실을 증가시키며, 두 손실 간에 진동(oscillation)이 발생해 학습 효율이 떨어지고 최종 해의 품질이 저하됨[19]
Dominating gradients in PINNs
두 기울기 크기의 극단적 불균형. \(\text{i.e.,} \|\nabla \mathcal{L}_r(\theta_t)\| ≪ \|\nabla \mathcal{L}_b(\theta_t)\|\ \text{or}\ \|\mathcal{L}_r(\theta_t)\|≫\|\nabla \mathcal{L}_b (\theta_t)\|\)
- 영향: 기울기가 큰 손실 항만 과도하게 최소화되고, 작은 기울기를 가진 손실은 사실상 무시됨. 이로 인해 수렴 속도 저하, 오버슈팅(overshooting)등이 발생하며, 더 중요한 손실이 학습되지 못할 가능성이 있음
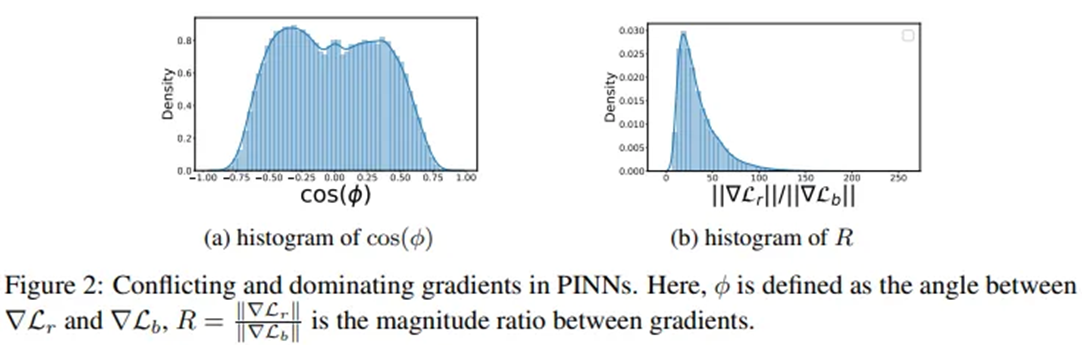
- 전체 반복의 약 절반에서 두 기울기가 충돌(conflicting)
- PDE 잔차 손실의 기울기가 BC 손실의 기울기보다 수십~수백 배 큰 경우가 흔하게 발생
Dual Cone Region
Dual Cone Region(Definition 4.1.):
주어진 cone \(\mathbf{K}_t\) 의 모든 벡터와 내적이 0 이상인 벡터들의 집합
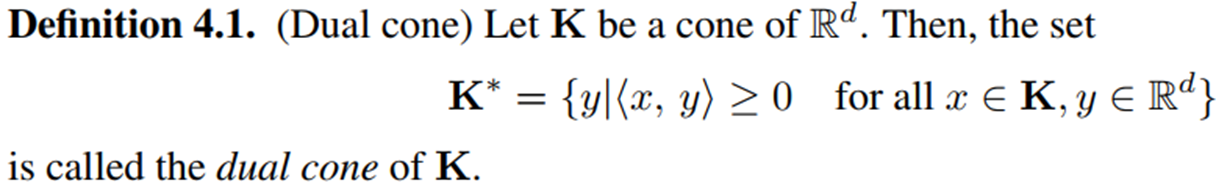
PINNs에 적용
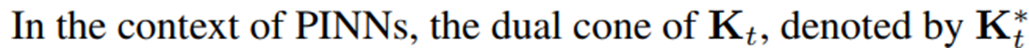
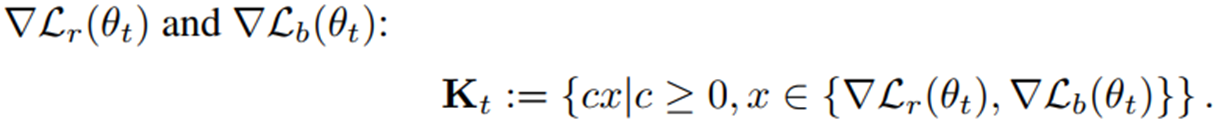
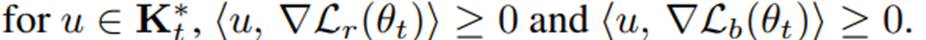
\(\mathbf{K}\) 는 PDE 잔차 손실 기울기와 경계 손실 기울기로 구성되어 있고, \(\mathbf{K^*}\) 는 PDE 잔차 손실과 경계 손실 기울기 모두와 내적이 0 이상인 벡터들의 집합이다.
\(\nabla \mathcal{L}(\theta_t)\in\mathbf{K}_t^{*}\) 인 경우, 적절한 학습률 하에서 두 손실이 동시에 감소한다.
\(\nabla \mathcal{L}(\theta_t)\notin \mathbf{K}_t^{*}\) 인 경우, 한 손실을 줄이는 업데이트가 다른 손실을 증가시킬 수 있다(역효과, adverse training).
Dual Cone에 속하는 조건 (Theorem 4.2.)
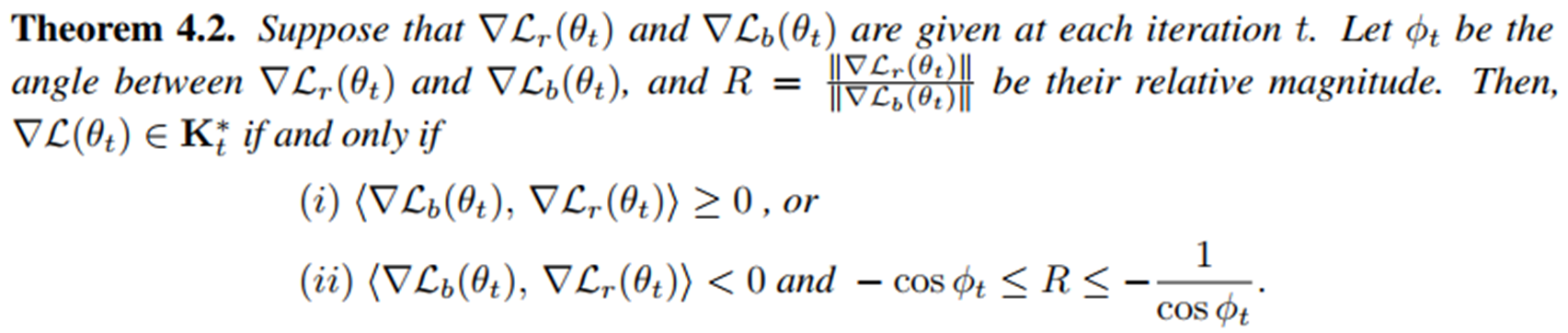
두 손실(PDE 잔차 손실, 경계 조건 손실)의 기울기 각도와 상대적 크기 관점에서 언제 총 기울기 \(\nabla \mathcal{L}(\theta_t)\) 가 Dual Cone에 포함되는지를 명확히 규정
이 정리는 기울기 충돌과 지배적 기울기의 문제를 수학적으로 정량화한다. 특히 각도 \(\phi_t\) 가 커질수록(더 충돌할수록), 작은 크기 불균형만으로도 학습이 실패할 수 있음을 보여준다.
Case (i) 증명 (두 기울기가 충돌하지 않는 경우)
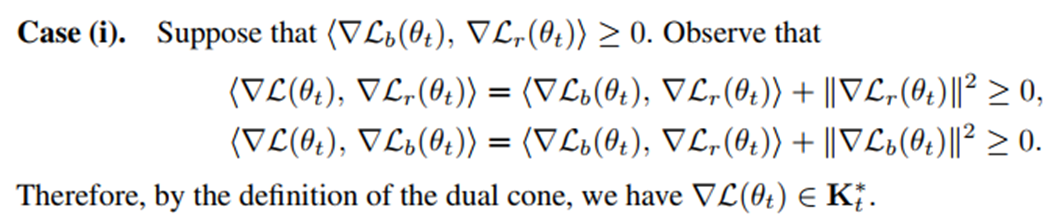
Case (ii) 증명 (두 기울기가 충돌하는 경우. 즉, \(90\degree<\phi \le 180\degree\))
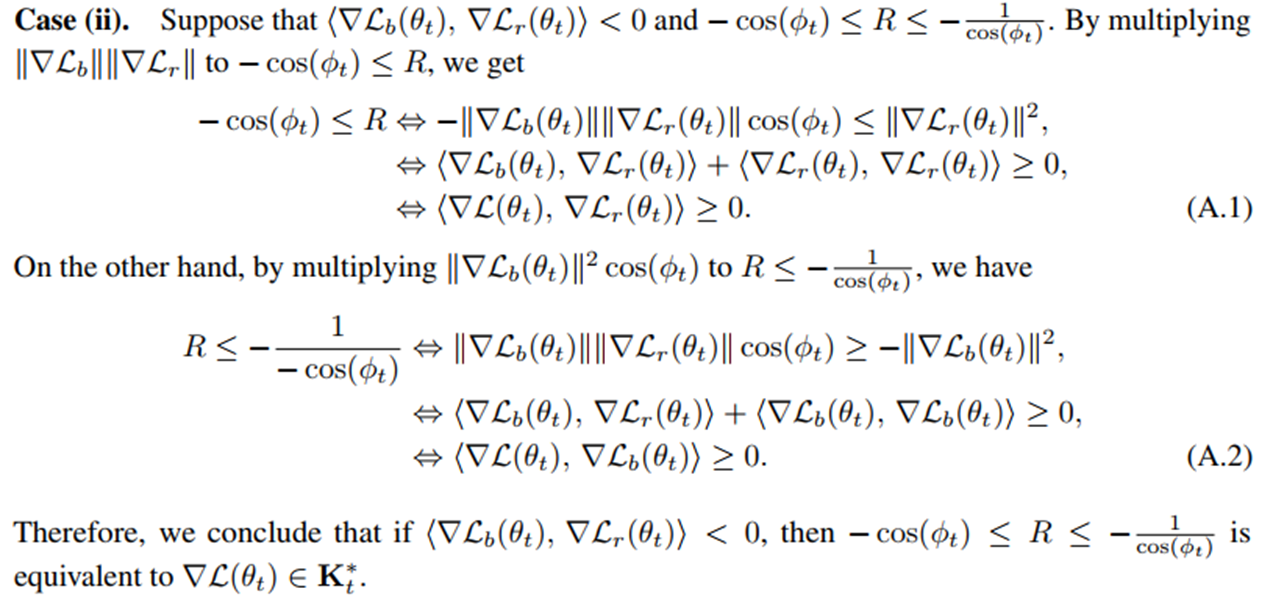
조건 해석
\(R\)이 너무 작으면 안 됨: \(R\ge -\text{cos}\phi_t \quad \nabla \mathcal{L}_r\) 이 너무 작으면 BC 기울기가 총합을 지배해 PDE 손실이 증가
\(R\)이 너무 크면 안 됨: \(R\le -1/\text{cos}\phi_t \quad \nabla \mathcal{L}_r\) 이 너무 크면 PDE 잔차 손실이 BC 손실을 덮어 BC 손실이 오히려 증가
결국 맨 아래 \(⟨\nabla \mathcal{L}, ∇\mathcal{L}_r(\theta_t)⟩ ≥ 0, ⟨\nabla \mathcal{L}, ∇\mathcal{L}_b(\theta_t)⟩ ≥ 0\) 로 전개된다는 것을 보면 됨.
충돌 상황에서는 기울기 비율이 각도에 따라 “허용 구간” 안에 있어야 Dual Cone에 들어간다.
Dominant Gradient와의 연관성
이 정리가 “Dominating Gradient”를 처음으로 명확히 수학적으로 정의한다.
예를 들어 \(\phi \approx 180 \degree\) (두 기울기가 완전히 반대)면:
\(-\text{cos} \phi \approx 1, \quad -1/\text{cos}\phi \rightarrow \infty\)
PDE가 너무 dominant하면 Dual Cone 밖으로 벗어남. 즉, 조금만 크기가 불균형해도 학습 실패
Dual Cone에 항상 포함되는 부분공간 정의 (Proposition 4.3.)
- Dual Cone \(\mathbf{K}_t^*\) 는 명시적으로 계산하기 어려워 \(\mathbf{K}_t^*\) 에 항상 포함되는 부분공간 \(\mathbf{G}_t\) 를 정의
Q&A
? 왜 Figure 1에서 PDE residual loss가 0부터 시작하는가?
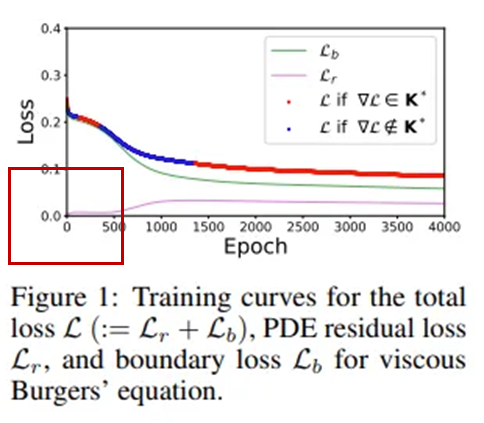
? BC loss가 0이 아닌 이유는?